Fonctions

Domaines de définition

L’ensemble de définition d’une fonction est l’ensemble A tel que :

$$\begin{array}{rl}f:& A\to B\\ & a\mapsto b\end{array}$$

Le tableau ci-après mentionne les domaines de définition des fonctions usuelles, ainsi que leurs dérivées

Fonction	Domaine de définition	Dérivée	Domaine dérivée	Condition particulière
k	$\mathbb{R}$	0	$\mathbb{R}$
$x^n$	$\mathbb{R}$	$n{x}^{n-1}$	$\mathbb{R}$	$n\in {\mathbb{N}}^{\ast }$
$\frac{1}{x^n}$	${\mathbb{R}}^{\ast }$	$-\frac{n}{x^{n+1}}$	${\mathbb{R}}^{\ast }$	$n\in {\mathbb{N}}^{\ast }$
$e^x$	$\mathbb{R}$	$e^x$	$\mathbb{R}$
$\ln x$	${\mathbb{R}}_{+}^{\ast }$	$\frac{1}{x}$	${\mathbb{R}}_{+}^{\ast }$
$\cos x$	$\mathbb{R}$	$-\sin x$	$\mathbb{R}$
$\sin x$	$\mathbb{R}$	$\cos x$	$\mathbb{R}$
$\sqrt{x}$	${\mathbb{R}}_{+}$	$\frac{1}{2\sqrt{x}}$	${\mathbb{R}}_{+}$

Parité des fonctions

Soit $f:A\to B$ une application.

• f est paire si : $\forall x\in A,-x\in A\text{ et }f(-x)=f(x)$
• f est impaire si : $\forall x\in A,-x\in A\text{ et }f(-x)=-f(x)$

Les graphes des fonctions paires et impaires possèdent une symétrie :

Type de fonction	Type de symétrie	Exemple de fonction	Graphe
Paire	par rapport à l’axe des ordonnées	$\cos ,|x|,$ les polynômes de degré pairs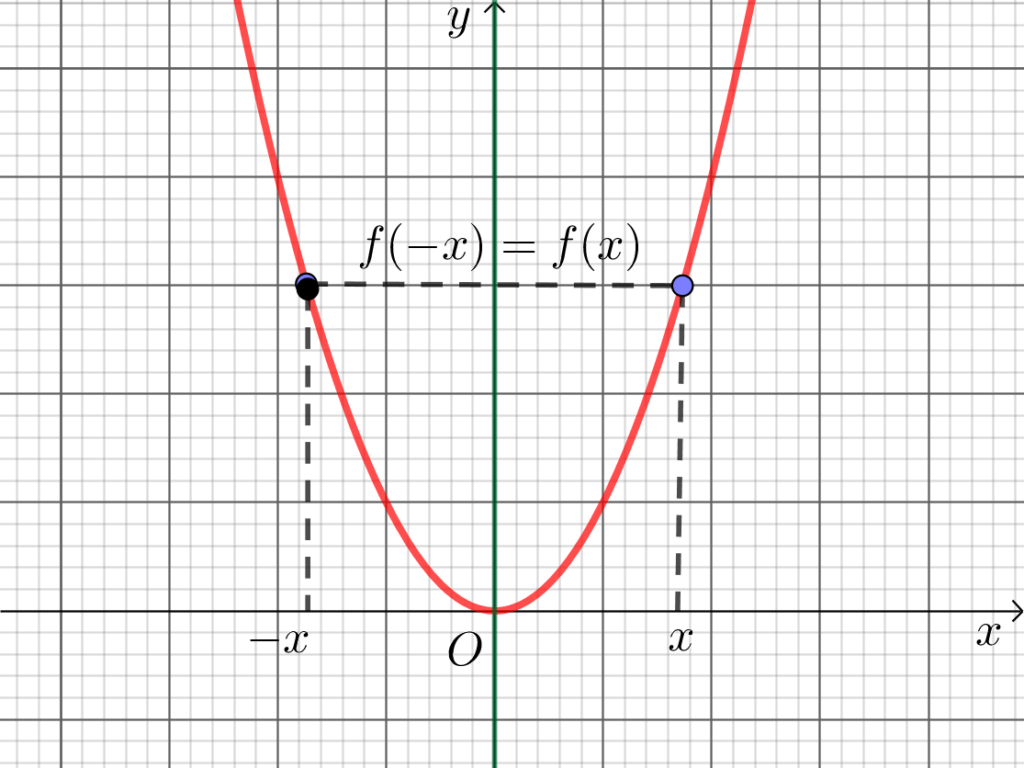
Impaire	centrale	$\sin$, les polynômes de degré impairs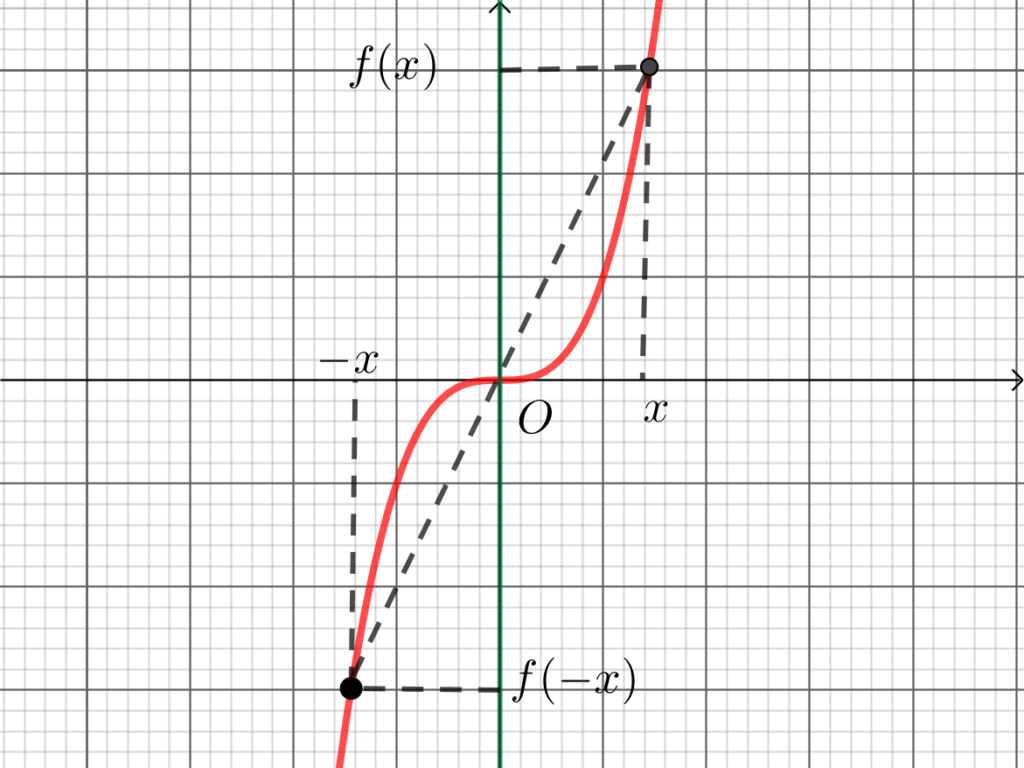

Injectivité, surjectivité, bijectivité

Soit $f:A\to B$ une application.

• f est injective si : $\forall x\in A,x^{\prime }\in A,f(x)=f(x^{\prime })\Rightarrow x=x^{\prime }$, c’est-à-dire qu’il existe au plus 1 seul $x\in A$ tel que $f(x)=y$
• f est surjective si : $\forall y\in B,\exists x\in A,f(x)=y$
• f est bijective si elle est injective et surjective

On peut le représenter ainsi :

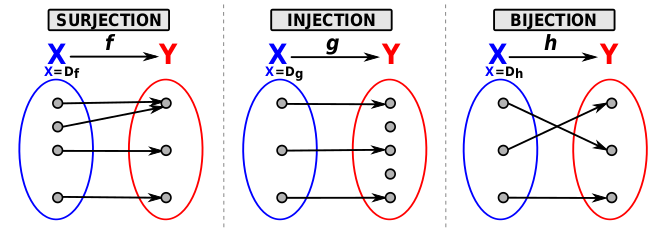
A partir d’une fonction bijective, on peut définir une fonction réciproque $f^{-1}$ (ou bijection réciproque) telle que : $f^{-1}A\to B$ et qui associe à chaque élément de l’ensemble d’arrivée son unique antécédent par $f$.

Pour déterminer cette fonction réciproque, on cherche $x$ tel que $f(x)=y$ avec $y\in B$ qui est donc l’antécédent de $x$ par $f$. Par exemple :

• $f(x)=3x+2$
• $y=3x+2$
• $y-2=3x$
• Donc finalement : $x=\frac{y-2}{3}=f^{-1}(y)$

Propriétés d’exemples de fonctions

Polynômes

Un polynôme à coefficients réels/complexes de degré $n$ s’écrit sous la forme : $P(X)=a_n{X}^n+a_{n-1}{X}^{n-1}+...a_{1}X+a_0$ avec $n\in \mathbb{N}$ et $a_i\in \mathbb{R}$

L’ensemble des polynômes réels s’écrit : $\mathbb{R}[X]$ et des polynômes complexes : $\mathbb{C}[X]$

Propriétés du degré d’un polynôme :

• Si $P=0$, $\text{deg}(P\cdot Q)=\text{deg}(P)+\text{deg}(Q)$