Nombres complexes

Formes des nombres complexes

• Forme algébrique : $z=a+bi$
• Forme trigonométrique : $z=|z|\times (\cos \theta +i\sin \theta )$
• Forme exponentielle : $z=|z|\times e^{i\theta }$

Pour passer de la forme algébrique à une autre, il faut calculer le module et l’argument.

Propriétés du module

Définition du module : $|z|=\sqrt{a^2+b^2}$

• $|z|=0⟺z=0$
• $|z|=|\overline{z}|=|-\overline{z}|=|-z|$
• $z\cdot \overline{z}=|z{|}^2$
• $|z\cdot \overline{z}|=|z|\cdot |\overline{z}|$ et donc $\left|\frac{z}{\overline{z}}\right|=\frac{|z|}{|\overline{z}|}$
• $\forall n\in \mathbb{N},|z^n|=|z{|}^n$
• Inégalité triangulaire : $|z+z^{\prime }|\le |z|+|z^{\prime }|$

Propriétés de l’argument

Définition de l’argument :

$$\begin{array}{c}\theta =arg(z)(mod(2\pi ))⟺\{\begin{array}{l}\cos \theta =\frac{Re(z)}{|z|}\\ \sin \theta =\frac{Im(z)}{|z|}\end{array}\end{array}$$

• $arg(\overline{z})=-arg(z)(mod2\pi )$
• $arg(-\overline{z})=\pi -arg(z)(mod2\pi )$
• $arg(z)=\pi +arg(z)(mod2\pi )$
• $arg(z\cdot z^{\prime })=arg(z)+arg(z^{\prime })(mod2\pi )$ et donc $arg\left(\frac{z}{z^{\prime }}\right)=arg(z)-arg(z^{\prime })(mod2\pi )$
• $\forall n\in \mathbb{N},arg(z^n)=n\cdot arg(z)(mod2\pi )$

Trigonométrie

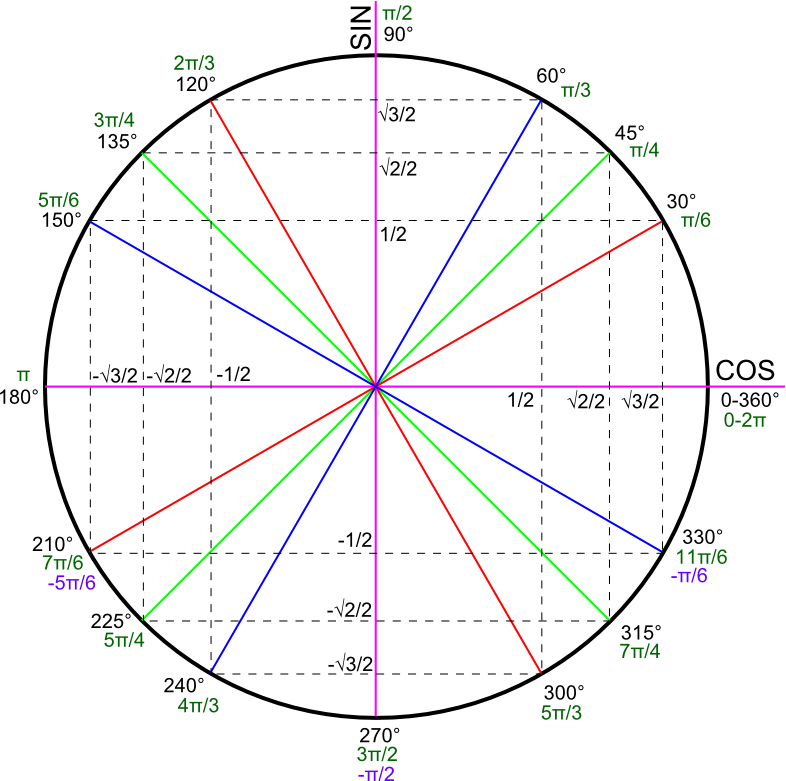
Formules de trigonométrie

Additions et soustractions :

• $\sin (a+b)=\sin a\cos b+\sin b\cos a$ et $\sin (a-b)=\sin a\cos b-\sin b\cos a$
• $\cos (a+b)=\cos a\cos b-\sin a\sin b$ et $\cos (a-b)=\cos a\cos b+\sin a\sin b$
• $\cos (a)\cos (b)=\frac{1}{2}(\cos (a+b)+\cos (a-b))$
• $\sin (a)\sin (b)=\frac{1}{2}(\cos (a-b)-\cos (a+b))$
• $\sin (a)\cos (b)=\frac{1}{2}(\sin (a+b)+\sin (a-b))$

Autres formules

$${\cos }^{2}a+{\sin }^{2}a=1$$

D’où les formules suivantes :

• $\cos (2a)={\cos }^{2}a-{\sin }^{2}a=2{\cos }^{2}a-1=1-2{\sin }^{2}a$
• $\sin (2a)=2\sin a\cos a$

Tangente : $\tan \theta =\frac{\sin \theta }{\cos \theta }$

• $\tan (a+b)=\frac{\tan a+\tan b}{1-\tan a\tan b}$
• $\tan (a-b)=\frac{\tan a-\tan b}{1+\tan a\tan b}$

Formule d’Euler, application aux nombres complexes

\cos\theta =\frac{e^{i\theta}+e^{-i\theta}}{2} \iff 2\cos\theta=e^{i\theta}+e^{-i\theta}$$

\sin\theta=\frac{e^{i\theta}-e^{-i\theta}}{2i} \iff 2i\sin\theta=e^{i\theta}-e^{-i\theta}

## Méthodes ### Linéarisation **Objectif :** Transformer des $\sin^{n}x$ et $\cos^{n}x$ en somme de $\sin(nx)$ et $\cos(nx)$ *Cela peut permettre de trouver des primitives par exemple* 1. Réecriture des $\sin^{n}x$ et $\cos^{n}x$ en utilisant la **formule d'Euler**

\cos^{n}\theta=\left(\frac{e^{i\theta}+e^{-i\theta}}{2}\right)^{n}

$$2.D\acute{e}veloppementaveclebin\hat{o}medeNewton:$$

\cos^{n}\theta=\frac{1}{2^{n}}\left(\sum_{k=0}^{n}\binom{n}{k}e^{i\theta(n-k)}\cdot e^{i\theta k} \right)

undefined

\begin{equation*} z^2=Z \iff \begin{cases} (x+iy)^{2}=a+ib \ |z|^{2}=|Z|= \sqrt{a^{2}+b^{2}} \end{cases} \iff \begin{cases} \textcolor{red}{x^{2}-y^{2}}+\textcolor{blue}{2xyi}=\textcolor{red}{a}+\textcolor{blue}{ib} \ x^2+y^2=\sqrt{a^{2}+b^{2}} \end{cases} \end{equation*}

On rassemble la partie $\textcolor{red}{\text{réelle}}$ et $\textcolor{blue}{\text{imaginaire}}$

\begin{equation*} z^2=Z \iff \begin{cases} \textcolor{red}{x^2-y^2=a} \ \textcolor{blue}{2xy=b} \ x^2+y^2=\sqrt{a^{2}+b^{2}} \end{cases} \end{equation*}

On peut alors facilement résoudre ce systèmes et trouver les racines de $z$ #### Polynôme de degré 2 avec coefficients complexes Pour résoudre une équation du type $az^{2}+bz+c=0$ avec $(a,b,c) \in \mathbb{C}$ : - Calculer $\Delta =b^{2}-4ac$ - Quelque soit $\Delta$, $\Delta$ admet deux racines oppposées telles que $\delta^2=\Delta$ - On trouve $\delta$ ([voir le paragraphe précédent](#Trouver%20les%20racines%20d'un%20nombre%20complexe)) et les solutions de l'équation sont donc : $z_{1}=\frac{-b-\delta}{2a}$ et $z_{2}=\frac{-b+\delta}{2a}$ #### Racines n-ièmes d'un nombre complexe L'équation $z^{n}=a$ possède $n$ solutions que l'on appelle les racines $n$-ièmes de $a$. Par exemple, pour $z^{2}=|z|\cdot e^{i\theta}$, ses racines sont $z_{1}=|z|^{1/2}e^{\frac{i\theta}{2}}$ et $z_{2}=|z|^{1/2}e^{i(\frac{\theta}{2}+\pi)}$ Pour trouver les racines $n$-ièmes, il faut trouver la racine évidente ($z_{1}=|z|^{1/n}e^{\frac{i\theta}{n}}$) et les racines $n$-ièmes de l'unité, c'est-à-dire, les solutions de : $w^{n}=1$ Les racines sont donc, avec $0 \leq k \leq n-1$, telles que :

\huge{|z|^{1/n}e^{i\left(\frac\theta{n}+\frac{2k\pi}n\right)}}