Introduction à la théorie des graphes

⇒ modélisation de problèmes à partir de graphes

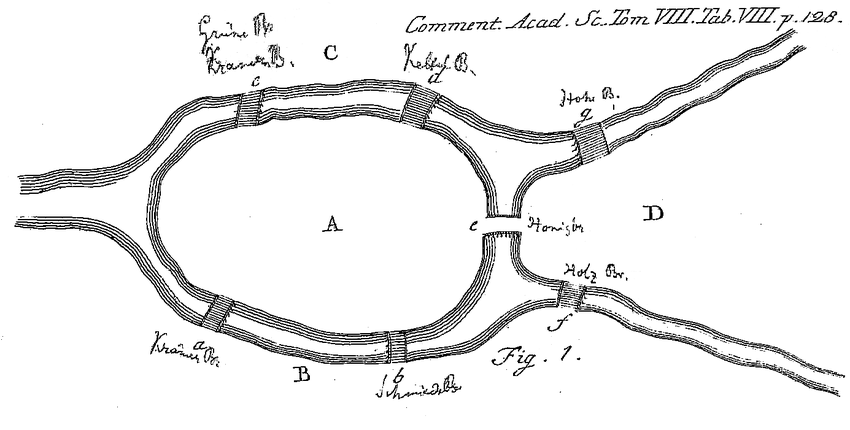
Problème des 7 ponts (1736, Euler)

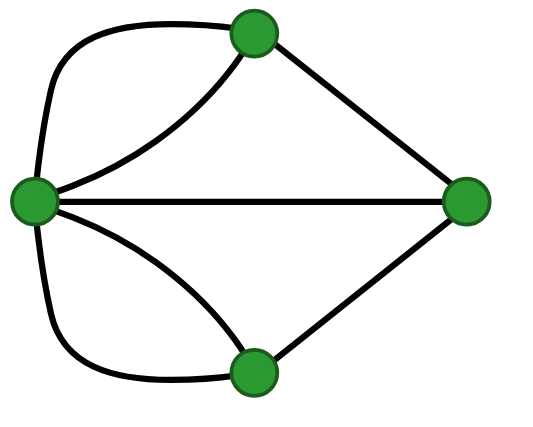
Le problème des sept ponts de Königsberg cherche à déterminer s’il existe un chemin permettant de revenir à son point de départ en empruntant une seule fois chaque pont de la ville ↪ modélisation par un graphe

C’est en fait impossible ⇒ à chacun des sommets il doit y avoir un nombre pair d’arrêtes

Utilité des graphes :

• création de réseaux (informatiques, eau…)
• trouver des chemins
• structures de données en informatique
• fonctionnement d’une cellule

Graphes orientés

Graphe orienté

Un graphe orienté est une paire $(S,A)$ composée d’un ensemble de sommets $S$ et d’une famille d’arcs $A$

L’ordre du graphe est le nombre de sommets $[S]$

L’ensemble des prédecesseurs de $a$ est noté ${\Gamma }^{-}(a)$ et l’ensemble des successeurs est noté ${\Gamma }^{+}(a)$ donc l’ensemble des voisins est : $\Gamma (a)={\Gamma }^{+}(a)\cup {\Gamma }^{-}(a)$

Famille

Ensemble dans lequel un élément peut apparaître plusieurs fois

Exemple

$G_1=(S_1,A_1)$ avec $S_1=\{1,2,3,4,5,6\}$ et $A_1=\{(1,2),(5,4),(1,4),(1,3),(2,1),(2,2),(3,4),(5,3),(5,4)\}$

   graph LR;
    1((1))-->2((2));
    5((5))-->4((4));
    1-->4;
    1-->3((3));
	 2-->1;
	 2-->2;
	 3-->4;
	 5-->3;
	 5-->4;
	 6((6));

Pour le sommet $1$, l’ensemble des successeurs est : ${\Gamma }^{+}(1)=\{2,3,4\}$ et ${\Gamma }^{-}(1)=\{2\}$

$p$-graphe

Graphe dans lequel un arc ne peut pas apparaître plus de $p$ fois

Graphes non orientés

Définiton

Graphe tel que $G_1=(S_1,A_1)$ où $S$ sont les sommets et $A$ les arrêtes ⇒ une arrête ne peut apparaître qu’une seule fois ($\ne$ aux arc dans les graphes orientés)

L’ensemble des voisins de $a$ est noté $\Gamma (a)$

Exemple

$S_1=\{1,2,3,4,5\}$ et $A_1=\{(1,2),(3,2),(1,4),(4,5)\}$

L’arrête $(1,2)$ est la même que l’arrête $(2,1)$. Cette arrête est incidente au sommet $1$ et $2$.

$\Gamma (1)=\{2,4\}$

   graph LR;
    1((1))---2((2));
    3((3))---2;
    1---4((4));
    4---5((5));

Degrés

Graphe orienté

Le demi-degré entrant d’un sommet $a$ est le nombre d’arcs de la forme $(.,a)$ (combien d’arrêtes arrivent à a) ⇒ noté $d^{-}(a)$

Le demi-degré sortant d’un sommet $a$ est le nombre d’arcs de la forme $(a,.)$ (combien d’arrêtes partent de a) ⇒ noté $d^{+}(a)$

Le degré de $a$ est $d=d^{-}(a)+d^{+}(a)$

Cas d'une boucle

Une boucle compte dans les deux catégories ⇒ demi-degré entrant et sortant (donc compte “double”)

Un sommet $a$ est :

• isolé si $d(a)=0$ ⇒ rien n’arrive ou ne part de $a$ (sommet 6)
• un puits si $d^{+}(a)=0$ ⇒ rien n’arrive à $a$ (sommet 4 et 6)
• une source si $d^{-}(a)=0$ ⇒ rien ne part de $a$ (sommet 5 et 6)

    graph LR;
    1((1))-->2((2));
    5((5))-->4((4));
    1-->4;
    1-->3((3));
	 2-->1;
	 2-->2;
	 3-->4;
	 5-->3;
	 5-->4;
	 6((6));

Graphe non orienté

Le degré d’un sommet $a$ est le nombre d’arrêtes contenant $a$.

De même, si $d(a)=0$ alors $a$ est un sommet isolé.

Chemins, circuits et cycles

graph LR;
    1((1));
    2((2));
    3((3));
    4((4));
    5((5));
    6((6));
    7((7));

	2-->1; 1-->5; 5-->4; 4-->3; 3-->7;

    1-->2;
    2-->1;
    1-->5;
    5-->4;
    4-->2;
    4-->3;
    3-->7;
    6-->6;
    6-->3;
    6-->7;
    7-->2;

linkStyle 0 stroke-width:2px,fill:none,stroke:red;
        linkStyle 1 stroke-width:2px,fill:none,stroke:red;
        linkStyle 2 stroke-width:2px,fill:none,stroke:red;
        linkStyle 3 stroke-width:2px,fill:none,stroke:red;
        linkStyle 4 stroke-width:2px,fill:none,stroke:red;
        linkStyle default stroke-width:2px,fill:none,stroke:black;
	

• $(2,1)(1,5)(5,4)(4,3)(3,7)$ ⇒ chemin simple et non fermé : toutes les arrêtes apparaissent une seule fois
• $(1,2)(2,1)(1,2)$ ⇒ chemin non simple et non fermé
• $(1,2)(2,1)(1,2)(2,1)$ ⇒ chemin non simple et non fermé

Circuit = chemin simple fermé

Hamiltonien ou eulérien

• Hamiltonien : passe exactement une fois par chaque sommet du graphe
• Eulérien : passe exactement une fois par chaque arrête ou arc du graphe

le problème EULÉRIEN de savoir si un graphe est eulérien est dans la classe P. Le problème HAMILTONIEN est a priori plus compliqué à résoudre algorithmiquement : c’est un problème NP-complet, avec des applications importantes.

Graphes partiels, sous-graphes, sous-graphes partiels

	Sous-graphe	Graphe partiel	Sous-graphe partiel
Sommets	Suppression	Conservés	Suppression
Arrêtes/arcs	Suppressions de ceux incidents des sommets	Suppression de certains	Suppression des incidents + des autres

Isomorphisme des graphes

⇒ veut dire que 2 graphes ont la même forme

En suivant la définition d’un graphe, ils peuvent être différents mais en fait ils ont la même forme.

Example

$G_1=\{\{1,2,3\},(1,2)(2,3)\}$ et $G_2=\{\{a,b,c\},(b,c)(c,a)\}$

graph LR
1((1))
2((2))
3((3))
a((a))
b((b))
c((c))
1-->2
2-->3
b-->c
c-->a

On voit que si l’on renomme les sommets, les graphes sont égaux

Une manière de définir l’isomorphisme est de définir une fonction de “renommage” des sommets ⇒ c’est une bijection

Définition : isomorphisme

$G_1=(S_1,A_1)$ et $G_2=(S_2,A_2)$ sont isomorphes s’il existe une bijection $f$ de $S_1\to S_2$ telle que : $(x,y)\in A_1⟺(f(x),f(y))\in A_2$