Représentation et Simplification des fonctions logiques

Réaliser un dispositif logique comporte plusieurs étapes :

1. Analyser le cahier des charges
2. Représenter le fonctionnement logique du système ⇒ utilisation des équations logiques booléennes (peut être utile de les simplifier)
3. Simplifier pour diminuer le nombre de circuits nécessaires
4. Réaliser le dispositif

Une fonction logique est représentable par :

• une table de vérité
• une/des expressions/s logiques
• une liste de nombres.

et elle peut être simplifiée par :

• la méthode algébrique
• la méthode de Karnaugh

Représentation des fonctions logiques

Par la table de vérité

Pour une fonction qui dépend de $n$ entrées, la table de vérité comporte $2^n$ lignes

Exemple d'une table de vérité

A partir de l’énoncé de ce problème : l’alarme se met en marche si la Pression est supérieure au seuil P₀ (condition P=1) ou si la pression est inférieure au seuil (condition P=0) et que la température est plus élevée que T₀ (condition T=1).

P	T	Alarme
0	0	0
0	1	1
1	0	1
1	1	1

Par une expression logique

A partir de la table de vérité, il faut considérer les combinaisons d’entrées pour lesquelles la sortie vaut 1

Exemple précédent

On a 3 combinaisons possibles, et cela correspond à la table de vérité du ET Donc la représentation par expression logique est $P\times T$

Somme de produits

À chaque sortie à 1, on obtient l’expression : $\overline{P}T+P\overline{T}+PT$ Cette forme de l’expression est appelée Somme de produits, qui permet de construire facilement le circuit à partir de portes ET, OU, NON

Cette représentation permet aussi de n’utiliser que des portes NAND

A partir de la forme Somme de produits de la fonction Alarme, donner l’expression et le circuit logique de cette fonction qui n’utilisent que des portes NAND à 2 entrées.

$\overline{P}T+P\overline{T}+PT=\overline{\overline{\overline{P}T+P\overline{T}+PT}}=??$

Formes canoniques

Les formes Somme de produit et Produit de sommes sont appelées les formes canoniques.

Pour la somme de produit (OU entre des ET) :

• Chaque produit logique doit contenir toutes les variables logiques, sous forme normale ou complémentée
• Cette forme de représentation permet assez directement de réaliser la fonction avec uniquement des portes NAND

Pour le produit de sommes (ET entre des OU) :

• Chaque somme logique doit contenir toutes les variables logiques, sous forme normale ou complémentée
• Cette forme de représentation permet assez directement de réaliser la fonction avec uniquement des portes NOR

Construire un produit de somme

1. Construire toutes les sommes logiques qui existent avec les variables dont dépend notre fonction
2. Faire le produit des sommes pour lesquelles la fonction vaut 0 (dans la table de vérité)

⇒ On ne conserve que les sommes logiques correspondant aux combinaisons pour lesquelles notre fonction (celle dont on cherche la forme canonique Produit de sommes) vaut 0

Donc dans l’exemple de l’alarme, le seul cas est pour $\overline{P}\times \overline{T}$ qui correspond au produit de somme (avec un seul facteur ici)

Par une liste de nombres

Aussi appelée représentation par des équivalents décimaux Surtout utilisé quand le nombre de variables devient important

• Définition d’un poids pour les variables (puissances de 2, en général le poids faibles et attribué à la variable la plus à droite)
• On remplace chaque produit logique par son équivalent décimal en utilisant le poids des variables
• La fonction est représentée par la liste des poids des produits qui sont présents dans la représentation somme de produits

Exemple

Une fonction $F(a,b,c,d)$ avec par exemple $2^3$ pour a, $2^2$ pour b, $2^1$ pour c et $2^0$ pour d Le poids d’un produit est donc la somme des poids des variables à 1 dans le produit : $\overline{a}b\overline{c}d=2^2+2^0=4+1=5$ et donc $\overline{abcd}=0$ Au lieu de dire que la fonction F vaut 1 pour les combinaisons (par exemple) abcd=0101 et abcd=1000 et abcd=1001 et abcd=1110, on peut écrire :

• F=1 pour (5, 8, 9, 14) ou encore
• F=(5, 8, 9, 14)

Donc l’écriture est plus concise

Exercice d’application

Donner la représentation sous forme somme de produits puis sous forme liste de nombres

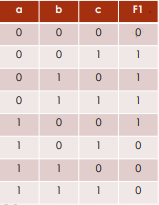
Forme somme de produit : $ab\overline{c}+a\overline{b}c+a\overline{b}\overline{c}+\overline{a}bc$

Poids : $a=4$, $b=2$,$c=1$ Donc $F_1$ vaut 1 pour :

• $001=1$
• $010=2$
• $011=3$
• $100=4$

Donc $F_1=(1,2,3,4)$

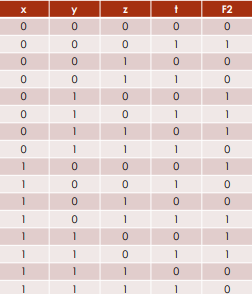
Forme somme de produits : $xyz\overline{t}+x\overline{y}zt+x\overline{y}z\overline{t}+x\overline{y}\overline{z}t+\overline{x}yzt+\overline{x}+y\overline{z}\overline{t}+\overline{x}\overline{y}zt+\overline{x}\overline{y}z\overline{t}$

Poids : $x=2^3=8$, $y=2^2=4$, $z=2$, $t=1$ Donc $F_2$ vaut 1 pour :

• 0001 = 1
• 0100 = 4
• 0101 = 5
• 0110 = 6
• 1000 = 8
• 1011 = 11
• 1100 = 12
• 1101 = 13

Donc $F_2=(1,4,5,6,8,11,12,13)$