Fiche de résolution d'équations et d'inéquations

I. Résolution d’équation

Définition

Une équation est une relation d’égalité, avec des inconnues, souvent notées $x$. Par exemple $2x=6$ ou $x+1=x$ sont des équations.

Quand certaines valeurs vérifient cette égalité, on dit que ces valeurs sont les solutions de l’équation. Par exemple, quand $x=3$, on a bien $2x=6$, donc $x=3$ est une solution de $2x=6$ On note ces solutions, avec $S$ l’ensemble des solutions : $S=so{l}_1,so{l}_2,...$ où $so{l}_1$ est une solution. Par exemple, on note $S=3$ pour $2x=6$

Quand aucune valeur ne vérifie cette égalité, on dit que l’équation n’a pas de solutions. Par exemple, $x+1=x$ revient à dire que $1=0$ ce qui est faux, donc $x+1=x$ n’a pas de solution. Dans ce cas-là, on écrit : $S=\varnothing$ ou $S=\text{{ }}$ , c’est-à-dire que $S$ est l’ensemble vide

Etapes de résolution d'équation

1. Vérification de l’existence de l’équation
2. Résolution de l’équation
3. Ecriture des solutions

1. Existence d’une équation

Une équation existe si elle a un sens mathématique. Par exemple, $\sqrt{-1}$ n’a pas de sens mathématiques dans les nombres réels. Donc l’équation $\sqrt{-x}$ n’existe pas si $x>0$.

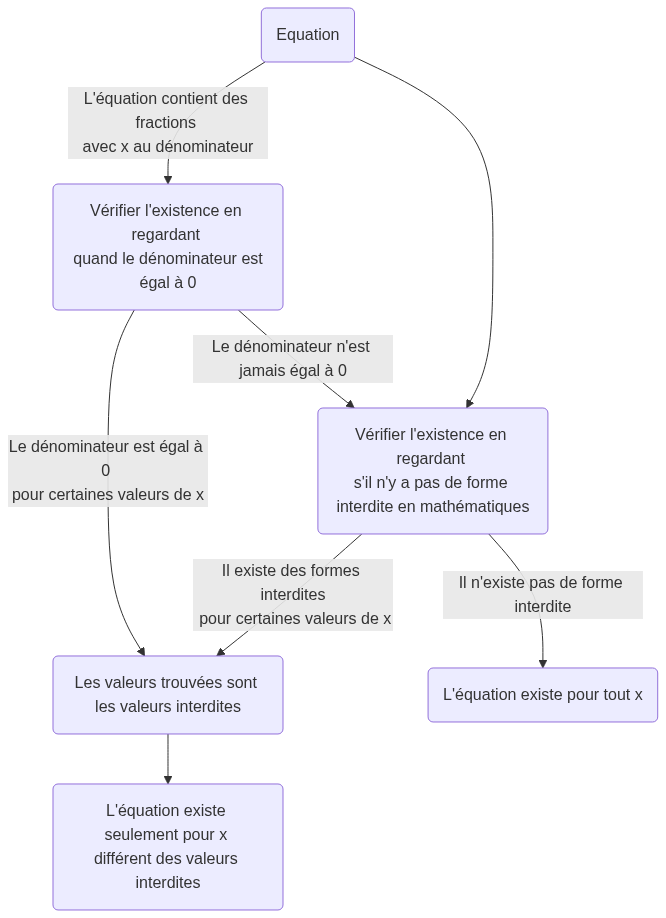
En général, on peut vérifier l’existence d’une équation avec le schéma suivant :

On notera l’ensemble de définition de l’équation, $D$ :

• $D=\mathbb{R}$ s’il n’y a pas de valeurs interdites
• $D=\mathbb{R}-\{\text{les valeurs interdites}\}$ ou $D=\mathbb{R}\setminus \{\text{les valeurs interdites}\}$

2. Résolution de l’équation

Résoudre une équation veut dire trouver les solutions de cette équation. Pour cela, on cherche à isoler l’inconnue, c’est-à-dire se retrouver avec une expression telle que $x=...$

Exemple de résolution de : \frac{x+1}{2}+\frac{x}{4x}=3

1. On met toutes les fractions au même dénominateur : $\frac{2x(x+1)+x}{4x}=3$
2. On multiplie par le dénominateur pour n’être plus sous forme de fraction : $2x^2+2x+x=3\times 4x$
3. On simplifie l’expression : $2x^2+3x=12x$
4. On rassemble les inconnues du même côté de l’égalité : $2x^2+3x-12x=12x-12x$ donc $2x^2-9x=0$
5. On factorise par $x$ : $x(2x-9)=0$
6. On applique la règle du produit nul : $x=0$, ou $2x-9=0⟺2x=9⟺x=\frac{9}{2}$

Le cas des fractions égales à 0

Si une équation contient une fraction égale à 0, par exemple $\frac{2x+1}{3x^2+4}=0$ alors la fraction est nulle si le numérateur est égal à 0.

Donc, il suffit de résoudre $\text{numeˊrateur}=0$, donc dans notre exemple : $2x+1=0⟺x=\frac{-1}{2}$

Les équations sans solutions

Si en résolvant une équation on aboutit à quelque chose de faux, alors l’équation n’a pas de solution Par exemple, dans le cas de $x+1=x$, en résolvant : $x+1-x=x-x⟺1=0$. Or, $1=0$ est faux, donc l’équation n’a pas de solution

Astuces à utiliser pour résoudre une équation

• Faire attention aux identités remarquables
• Essayer de factoriser pour pouvoir appliquer la règle du produit nul
• Multiplier par le dénominateur pour pouvoir résoudre l’équation
• Simplifier l’écriture pour éviter les erreurs de calcul

3. Écriture des solutions

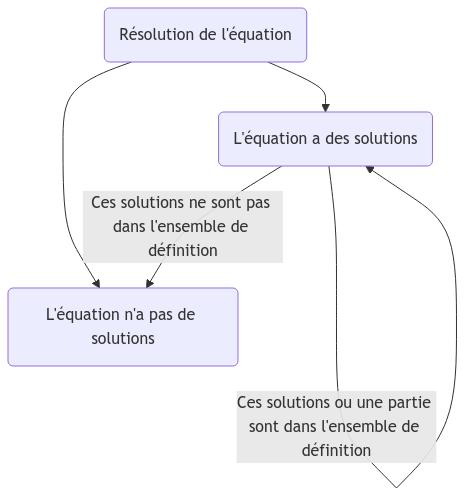
Pour écrire les solutions, on peut suivre ce schéma :

Donc il est important de vérifier la présence des solutions trouvées dans l’ensemble de définition défini à l’étape 1.

Exemple de cas où il y a des solutions qui ne sont pas dans l'ensemble de définition

L’équation $\frac{4x+12}{x+3}=0$ a pour ensemble de définition $D=\mathbb{R}-\{-3\}$ car $-3+3=0$

Si on résout l’équation : $\frac{4x+12}{x+3}=0⟺4x+12=0⟺4x=-12⟺x=\frac{-12}{4}=-3$

Donc les solutions de l’équations sont $-3$. Mais $-3$ n’est pas dans l’ensemble de définition. Donc il n’y a pas de solutions : $S=\{\}$

II. Résolution d’inéquation

Définition

Une inéquation est une relation d’inégalité, avec des inconnues, souvent notées $x$. Par exemple $2x<6$ ou $x+1\le x$ sont des équations.

Quand certaines valeurs vérifient cette inégalité, on dit que ces valeurs sont les solutions de l’inéquation. Par exemple, quand $x<3$, on a bien $2x<6$, donc $x<3$ est une solution de $2x<6$ On note ces solutions sous forme d’un intervalle ou d’une réunion d’intervalle, avec $S$ l’ensemble des solutions : $S=[-\infty ;so{l}_1]$ où $x<so{l}_1$ est une solution. Par exemple, on note $S=[-\infty ;3]$ pour $2x=6$

Quand aucune valeur ne vérifie cette inégalité, on dit que l’inéquation n’a pas de solutions.

Etapes de résolution d'une inéquation

Ce sont les mêmes que pour une équation :

1. Vérification de l’existence de l’inéquation
2. Résolution de l’inéquation
3. Ecriture des solutions

La seule différence avec les équations se fait sur les règles de résolution de l’inéquation, et sur l’écriture des solutions

Règles de résolution d'une inéquation

Quand on multiplie ou on divise par un nombre négatif on doit changer le sens de l’inéquation (tout en conservant la stricte inégalité $<,>$ ou non $\le ,\ge$). Par exemple, $-2x<10⟺\frac{-2x}{-2}>\frac{10}{-2}⟺x>-5$

Ecriture des solutions d'une inéquation

On écrit les solutions sous forme d’intervalle. Si une valeur interdite se trouve au sein de cet intervalle, on exclut uniquement cette valeur.

Par exemple, si $6$ n’appartient pas au domaine de définition et que les solutions sont dans l’intervalle $[0,10]$, alors les solutions de l’inéquation sont : $[0;6[\cup ]6;10]$