Forme algébrique : z = a + b i z = a+bi z = a + bi Forme trigonométrique : z = ∣ z ∣ × ( cos θ + i sin θ ) z= |z| \times (\cos{\theta}+i\sin{\theta}) z = ∣ z ∣ × ( cos θ + i sin θ ) Forme exponentielle : z = ∣ z ∣ × e i θ z = |z|\times e^{i\theta} z = ∣ z ∣ × e i θ
Pour passer de la forme algébrique à une autre, il faut calculer le module et l’argument.
Définition du module : ∣ z ∣ = a 2 + b 2 |z| =\sqrt{a^2+b^2} ∣ z ∣ = a 2 + b 2
∣ z ∣ = 0 ⟺ z = 0 |z| = 0 \iff z=0 ∣ z ∣ = 0 ⟺ z = 0 ∣ z ∣ = ∣ z ‾ ∣ = ∣ − z ‾ ∣ = ∣ − z ∣ |z|=|\overline{z}|= |-\overline{z}|=|-z| ∣ z ∣ = ∣ z ∣ = ∣ − z ∣ = ∣ − z ∣ z ⋅ z ‾ = ∣ z ∣ 2 z\cdot \overline{z} = |z|^2 z ⋅ z = ∣ z ∣ 2 ∣ z ⋅ z ‾ ∣ = ∣ z ∣ ⋅ ∣ z ‾ ∣ |z\cdot \overline{z}| = |z|\cdot|\overline{z}| ∣ z ⋅ z ∣ = ∣ z ∣ ⋅ ∣ z ∣ ∣ z z ‾ ∣ = ∣ z ∣ ∣ z ‾ ∣ \left|\frac{z}{\overline{z}} \right|= \frac{|z|}{|\overline{z}|} z z = ∣ z ∣ ∣ z ∣ ∀ n ∈ N , ∣ z n ∣ = ∣ z ∣ n \forall n \in \mathbb{N}, |z^n|=|z|^{n} ∀ n ∈ N , ∣ z n ∣ = ∣ z ∣ n Inégalité triangulaire : ∣ z + z ′ ∣ ≤ ∣ z ∣ + ∣ z ′ ∣ |z+z'| \leq |z|+|z'| ∣ z + z ′ ∣ ≤ ∣ z ∣ + ∣ z ′ ∣
Définition de l’argument :
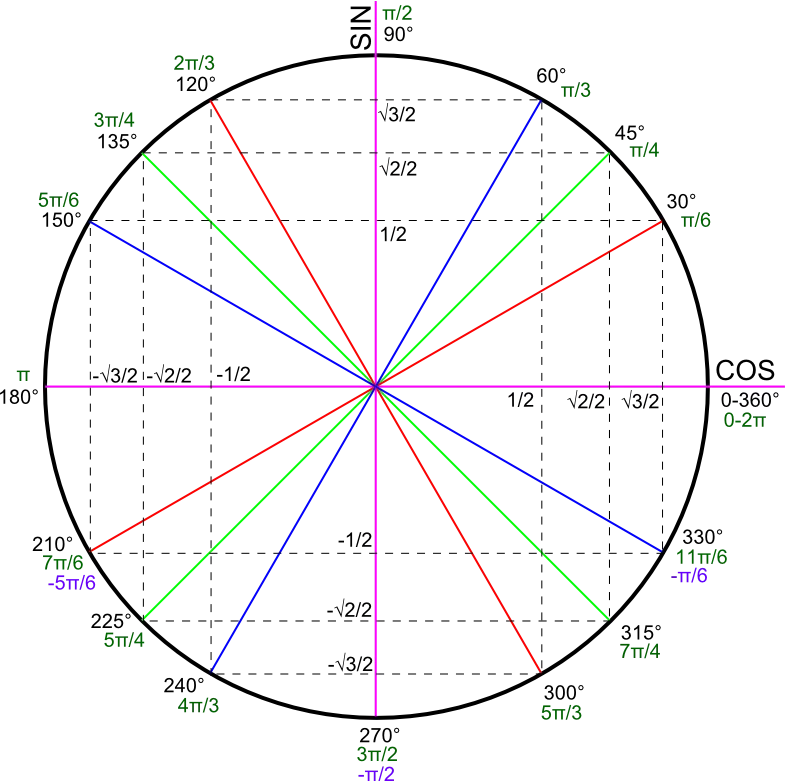
θ = a r g ( z ) ( m o d ( 2 π ) ) ⟺ { cos θ = R e ( z ) ∣ z ∣ sin θ = I m ( z ) ∣ z ∣ \begin{equation*}
\theta = arg(z)(mod(2\pi)) \iff
\begin{cases}
\cos{\theta}=\frac{Re(z)}{|z|} \\
\sin{\theta}=\frac{Im(z)}{|z|}
\end{cases}
\end{equation*} θ = a r g ( z ) ( m o d ( 2 π )) ⟺ { cos θ = ∣ z ∣ R e ( z ) sin θ = ∣ z ∣ I m ( z )
a r g ( z ‾ ) = − a r g ( z ) ( m o d 2 π ) arg(\overline{z}) =-arg(z) (mod~2\pi) a r g ( z ) = − a r g ( z ) ( m o d 2 π ) a r g ( − z ‾ ) = π − a r g ( z ) ( m o d 2 π ) arg(-\overline{z}) =\pi-arg(z) (mod~2\pi) a r g ( − z ) = π − a r g ( z ) ( m o d 2 π ) a r g ( z ) = π + a r g ( z ) ( m o d 2 π ) arg(z) =\pi+arg(z) (mod~2\pi) a r g ( z ) = π + a r g ( z ) ( m o d 2 π ) a r g ( z ⋅ z ′ ) = a r g ( z ) + a r g ( z ′ ) ( m o d 2 π ) arg(z\cdot z')=arg(z)+arg(z')(mod~2\pi) a r g ( z ⋅ z ′ ) = a r g ( z ) + a r g ( z ′ ) ( m o d 2 π ) a r g ( z z ′ ) = a r g ( z ) − a r g ( z ′ ) ( m o d 2 π ) arg\left(\frac{z}{z'} \right)= arg(z)-arg(z')(mod~2\pi) a r g ( z ′ z ) = a r g ( z ) − a r g ( z ′ ) ( m o d 2 π ) ∀ n ∈ N , a r g ( z n ) = n ⋅ a r g ( z ) ( m o d 2 π ) \forall n \in \mathbb{N}, arg(z^{n})=n\cdot arg(z)(mod~2\pi) ∀ n ∈ N , a r g ( z n ) = n ⋅ a r g ( z ) ( m o d 2 π )
Additions et soustractions :
sin ( a + b ) = sin a cos b + sin b cos a \sin(a+b) = \sin{a}\cos{b} + \sin{b}\cos{a} sin ( a + b ) = sin a cos b + sin b cos a sin ( a − b ) = sin a cos b − sin b cos a \sin(a-b)=\sin{a}\cos{b}-\sin{b}\cos{a} sin ( a − b ) = sin a cos b − sin b cos a cos ( a + b ) = cos a cos b − sin a sin b \cos(a+b)=\cos{a}\cos{b}-\sin{a}\sin{b} cos ( a + b ) = cos a cos b − sin a sin b cos ( a − b ) = cos a cos b + sin a sin b \cos(a-b)=\cos{a}\cos{b}+\sin{a}\sin{b} cos ( a − b ) = cos a cos b + sin a sin b cos ( a ) cos ( b ) = 1 2 ( cos ( a + b ) + cos ( a − b ) ) \cos(a)\cos(b)=\frac{1}{2}(\cos(a+b)+\cos(a-b)) cos ( a ) cos ( b ) = 2 1 ( cos ( a + b ) + cos ( a − b )) sin ( a ) sin ( b ) = 1 2 ( cos ( a − b ) − cos ( a + b ) ) \sin(a)\sin(b)=\frac{1}{2}(\cos(a-b)-\cos(a+b)) sin ( a ) sin ( b ) = 2 1 ( cos ( a − b ) − cos ( a + b )) sin ( a ) cos ( b ) = 1 2 ( sin ( a + b ) + sin ( a − b ) ) \sin(a)\cos(b)=\frac{1}{2}(\sin(a+b)+\sin(a-b)) sin ( a ) cos ( b ) = 2 1 ( sin ( a + b ) + sin ( a − b ))
Autres formules
cos 2 a + sin 2 a = 1 \cos^{2}a+ \sin^{2}a= 1 cos 2 a + sin 2 a = 1 D’où les formules suivantes :
cos ( 2 a ) = cos 2 a − sin 2 a = 2 cos 2 a − 1 = 1 − 2 sin 2 a \cos(2a)=\cos^2a-\sin^{2}a=2\cos^2a-1=1-2\sin^2a cos ( 2 a ) = cos 2 a − sin 2 a = 2 cos 2 a − 1 = 1 − 2 sin 2 a sin ( 2 a ) = 2 sin a cos a \sin(2a)=2\sin{a}\cos{a} sin ( 2 a ) = 2 sin a cos a
Tangente : tan θ = sin θ cos θ \tan\theta =\frac{\sin\theta}{\cos\theta} tan θ = c o s θ s i n θ
tan ( a + b ) = tan a + tan b 1 − tan a tan b \tan(a+b)=\frac{\tan{a}+\tan{b}}{1-\tan{a}\tan{b}} tan ( a + b ) = 1 − t a n a t a n b t a n a + t a n b tan ( a − b ) = tan a − tan b 1 + tan a tan b \tan(a-b)=\frac{\tan{a}-\tan{b}}{1+\tan{a}\tan{b}} tan ( a − b ) = 1 + t a n a t a n b t a n a − t a n b
Formule d’Euler, application aux nombres complexes
cos θ = e i θ + e − i θ 2 ⟺ 2 cos θ = e i θ + e − i θ \cos\theta =\frac{e^{i\theta}+e^{-i\theta}}{2} \iff 2\cos\theta=e^{i\theta}+e^{-i\theta} cos θ = 2 e i θ + e − i θ ⟺ 2 cos θ = e i θ + e − i θ sin θ = e i θ − e − i θ 2 i ⟺ 2 i sin θ = e i θ − e − i θ \sin\theta=\frac{e^{i\theta}-e^{-i\theta}}{2i} \iff 2i\sin\theta=e^{i\theta}-e^{-i\theta} sin θ = 2 i e i θ − e − i θ ⟺ 2 i sin θ = e i θ − e − i θ Objectif : Transformer des sin n x \sin^{n}x sin n x cos n x \cos^{n}x cos n x sin ( n x ) \sin(nx) sin ( n x ) cos ( n x ) \cos(nx) cos ( n x ) Cela peut permettre de trouver des primitives par exemple
Réecriture des sin n x \sin^{n}x sin n x cos n x \cos^{n}x cos n x formule d’Euler
cos n θ = ( e i θ + e − i θ 2 ) n \cos^{n}\theta=\left(\frac{e^{i\theta}+e^{-i\theta}}{2}\right)^{n} cos n θ = ( 2 e i θ + e − i θ ) n
Développement avec le binôme de Newton :
cos n θ = 1 2 n ( ∑ k = 0 n ( n k ) e i θ ( n − k ) ⋅ e i θ k ) \cos^{n}\theta=\frac{1}{2^{n}}\left(\sum_{k=0}^{n}\binom{n}{k}e^{i\theta(n-k)}\cdot e^{i\theta k} \right) cos n θ = 2 n 1 ( k = 0 ∑ n ( k n ) e i θ ( n − k ) ⋅ e i θ k )
Regroupement des exponentielles de même puissance. *Par exemple : c o s 3 x = 1 8 ( e 3 i x + 3 e i x + 3 e − i x + e − 3 i x ) ⟺ 1 8 ( e 3 i x + e − 3 i x + 3 ( e i x + e − i x ) ) cos^{3}x=\frac{1}{8}(e^{3ix}+3e^{ix}+3e^{-ix}+e^{-3ix})\iff \frac{1}{8}(e^{3ix}+e^{-3ix}+3(e^{ix}+e^{-ix})) co s 3 x = 8 1 ( e 3 i x + 3 e i x + 3 e − i x + e − 3 i x ) ⟺ 8 1 ( e 3 i x + e − 3 i x + 3 ( e i x + e − i x ))
Réutilisation des formules d’Euler 2 cos θ = e i θ + e − i θ 2\cos\theta=e^{i\theta}+e^{-i\theta} 2 cos θ = e i θ + e − i θ 2 i sin θ = e i θ − e − i θ 2i\sin\theta=e^{i\theta}-e^{-i\theta} 2 i sin θ = e i θ − e − i θ Par exemple : c o s 3 x = 1 8 ( 2 cos ( 3 x ) + 3 ⋅ 2 cos ( x ) ) cos^{3}x=\frac{1}{8}(2\cos(3x)+3\cdot2\cos(x)) co s 3 x = 8 1 ( 2 cos ( 3 x ) + 3 ⋅ 2 cos ( x ))
Simplification par 2
Attention pour la linéarisation des sinus
Ne pas oublier les i , aussi bien dans les 1 ( 2 i ) n \frac{1}{(2i)^n} ( 2 i ) n 1 2 i sin θ = e i θ − e − i θ 2i\sin\theta=e^{i\theta}-e^{-i\theta} 2 i sin θ = e i θ − e − i θ
On peut aussi utiliser les formules de trigonométrie usuelles pour linéariser.
On cherche z z z z 2 = Z z^{2}=Z z 2 = Z z = x + i y z=x+iy z = x + i y Z = a + b i Z=a+bi Z = a + bi ( a , b ) ∈ R (a,b)\in \mathbb{R} ( a , b ) ∈ R
Pour trouver x et y x \text{ et } y x et y
z 2 = Z ⟺ { ( x + i y ) 2 = a + i b ∣ z ∣ 2 = ∣ Z ∣ = a 2 + b 2 ⟺ { x 2 − y 2 + 2 x y i = a + i b x 2 + y 2 = a 2 + b 2 \begin{equation*}
z^2=Z \iff
\begin{cases}
(x+iy)^{2}=a+ib \\
|z|^{2}=|Z|= \sqrt{a^{2}+b^{2}}
\end{cases}
\iff
\begin{cases}
\textcolor{red}{x^{2}-y^{2}}+\textcolor{blue}{2xyi}=\textcolor{red}{a}+\textcolor{blue}{ib} \\
x^2+y^2=\sqrt{a^{2}+b^{2}}
\end{cases}
\end{equation*} z 2 = Z ⟺ { ( x + i y ) 2 = a + ib ∣ z ∣ 2 = ∣ Z ∣ = a 2 + b 2 ⟺ { x 2 − y 2 + 2 x y i = a + ib x 2 + y 2 = a 2 + b 2 On rassemble la partie r e ˊ elle \textcolor{red}{\text{réelle}} r e ˊ elle imaginaire \textcolor{blue}{\text{imaginaire}} imaginaire
z 2 = Z ⟺ { x 2 − y 2 = a 2 x y = b x 2 + y 2 = a 2 + b 2 \begin{equation*}
z^2=Z \iff
\begin{cases}
\textcolor{red}{x^2-y^2=a} \\
\textcolor{blue}{2xy=b} \\
x^2+y^2=\sqrt{a^{2}+b^{2}}
\end{cases}
\end{equation*} z 2 = Z ⟺ ⎩ ⎨ ⎧ x 2 − y 2 = a 2 x y = b x 2 + y 2 = a 2 + b 2 On peut alors facilement résoudre ce systèmes et trouver les racines de z z z
Pour résoudre une équation du type a z 2 + b z + c = 0 az^{2}+bz+c=0 a z 2 + b z + c = 0 ( a , b , c ) ∈ C (a,b,c) \in \mathbb{C} ( a , b , c ) ∈ C
Calculer Δ = b 2 − 4 a c \Delta =b^{2}-4ac Δ = b 2 − 4 a c
Quelque soit Δ \Delta Δ Δ \Delta Δ δ 2 = Δ \delta^2=\Delta δ 2 = Δ
On trouve δ \delta δ voir le paragraphe précédent ) et les solutions de l’équation sont donc : z 1 = − b − δ 2 a z_{1}=\frac{-b-\delta}{2a} z 1 = 2 a − b − δ z 2 = − b + δ 2 a z_{2}=\frac{-b+\delta}{2a} z 2 = 2 a − b + δ
L’équation z n = a z^{n}=a z n = a n n n n n n a a a z 2 = ∣ z ∣ ⋅ e i θ z^{2}=|z|\cdot e^{i\theta} z 2 = ∣ z ∣ ⋅ e i θ z 1 = ∣ z ∣ 1 / 2 e i θ 2 z_{1}=|z|^{1/2}e^{\frac{i\theta}{2}} z 1 = ∣ z ∣ 1/2 e 2 i θ z 2 = ∣ z ∣ 1 / 2 e i ( θ 2 + π ) z_{2}=|z|^{1/2}e^{i(\frac{\theta}{2}+\pi)} z 2 = ∣ z ∣ 1/2 e i ( 2 θ + π )
Pour trouver les racines n n n z 1 = ∣ z ∣ 1 / n e i θ n z_{1}=|z|^{1/n}e^{\frac{i\theta}{n}} z 1 = ∣ z ∣ 1/ n e n i θ n n n w n = 1 w^{n}=1 w n = 1
Les racines sont donc, avec 0 ≤ k ≤ n − 1 0 \leq k \leq n-1 0 ≤ k ≤ n − 1
∣ z ∣ 1 / n e i ( θ n + 2 k π n ) \huge{|z|^{1/n}e^{i\left(\frac\theta{n}+\frac{2k\pi}n\right)}} ∣ z ∣ 1/ n e i ( n θ + n 2 kπ )