# Fiche de résolution d'équations et d'inéquations
Table of Contents
I. Résolution d’équation
1. Existence d’une équation
Une équation existe si elle a un sens mathématique. Par exemple, n’a pas de sens mathématiques dans les nombres réels. Donc l’équation n’existe pas si .
En général, on peut vérifier l’existence d’une équation avec le schéma suivant :
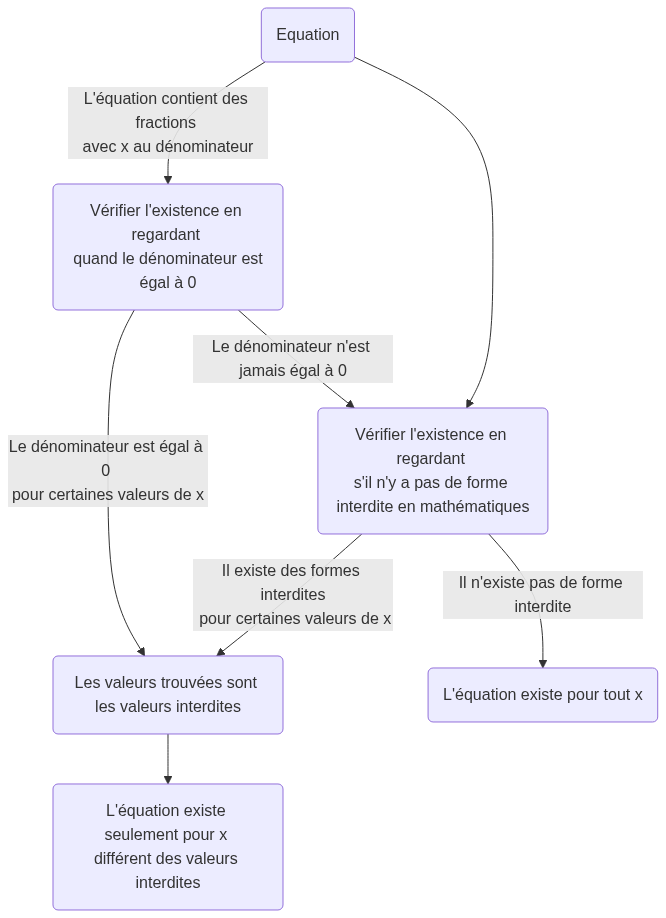
On notera l’ensemble de définition de l’équation, :
- s’il n’y a pas de valeurs interdites
- ou
2. Résolution de l’équation
Résoudre une équation veut dire trouver les solutions de cette équation. Pour cela, on cherche à isoler l’inconnue, c’est-à-dire se retrouver avec une expression telle que
3. Écriture des solutions
Pour écrire les solutions, on peut suivre ce schéma :
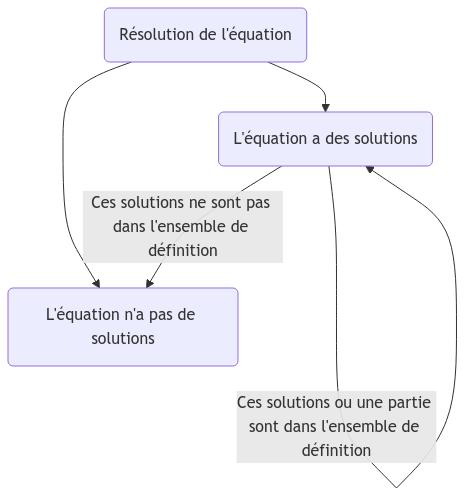
Donc il est important de vérifier la présence des solutions trouvées dans l’ensemble de définition défini à l’étape 1.
II. Résolution d’inéquation
La seule différence avec les équations se fait sur les règles de résolution de l’inéquation, et sur l’écriture des solutions