Table of Contents
Introduction
Dans Numération : représentation des nombres, on a vu la représentation générale des nombres dans toutes les bases
On va voir ici comment les nombres sont codés dans un ordinateur : le format nombres.
- Limitations physiques (tailles des “mots” limités : 16, 32 ou 64 bits donc nombre d’octects fixes)
- Traiter les nombres négatifs (nombres signés) —> entiers signés (int) (les entiers non signés sont uint)
- Traiter les nombres réels (float ou double)
==Le format donne le type des nombres==
Représentation DCB - Décimal Codé Binaire
Définition
S’utilise principalement pour les systèmes d’affichages des valeurs numériques et dans les machines à calculer.
Chaque chiffre décimal (de 0 à 9) est codé sur 4 bits (voir pour le passage en binaire)
| Poids | ||||
|---|---|---|---|---|
| N | ||||
| 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 1 |
| 2 | 0 | 0 | 1 | 0 |
| 3 | 0 | 0 | 1 | 1 |
| 4 | 0 | 1 | 0 | 0 |
| 5 | 0 | 1 | 0 | 1 |
| 6 | 0 | 1 | 1 | 0 |
| 7 | 0 | 1 | 1 | 1 |
| 8 | 1 | 0 | 0 | 0 |
| 9 | 1 | 0 | 0 | 1 |
::: caution[Etats invalides] Comme on ne veut coder que des chiffres, il existe des états interdits (qui correspondraient aux valeurs de 10 à 15) Les états interdits en DCB : 1010, 1011, 1100, 1101, 1110, 1111 :::
::: tip[Passer du décimal en DCB] 518 en DCB : 0101 0000 1000 139 en DCB : 0001 0011 1001 :::
Toujours un multiple de 4 bits en DCB
Conversion et lecture très facile mais très gourmand en espace mémoire (car consomme énormément de bits)
::: tip[Consommation en mémoire] Pour 1024 états : 16 bits en DCB alors que donc seulement 10 bits en binaire :::
Opérations
1er cas : la somme est < 9
On ne se trouve pas sur un état interdit
::: tip[Exemple de calcul : opération facile]
- 35 + 24 en DCB
- 35 = 0011 0101
- 24 = 0010 0100
- La somme est = 0101 1001 (DCB)
- On peut vérifier car 0101 = 5 et 1001 = 9 donc on a bien 59 :::
::: caution[Ne pas confondre le format et la numération] Format = DCB Numération = décimal Les règles ne sont pas les mêmes ! :::
2ème cas : la somme est > 9
On passe par les états interdits
- Le résultat est un état invalide ↪ passer les 6 états invalides (donc ajouter 6)
- Retenu sur le paquet de 4 bits suivants (+6) mais le résultat n’est pas invalide
::: tip[Premier cas : état invalide]
- 6+7 en DCB
- 0110 + 0111 = 1101 = état invalide donc faux
- On ajoute 6 pour passer les états interdits (pour passer de 9 à 10 = 1 et 0 = 0001 0000 (DCB))
- 1101 + 0110 = 10011 donc le résultat est : 0001 0011 donc 13 :::
::: tip[Deuxième cas : pas invalide]
- 8+ 9 en DCB
- 1000 + 1001 = 10001 = pas un état invalide —> retenue
- Donc tous les états interdits ont été comptés : il faut donc rajouter 6 pour passer les états interdits
- 10001 + 0110 = 10111 donc le résultat est 0001 0111 donc 17 :::
Représentation des nombres entiers signés ↪ complément à 2
Nombres entiers signés = nombres positifs et négatifs
Compléments à 2
Définition
==Format pour représenter les nombres entiers==
Ce format (cpt2) est à nombre de bits fixé (16, 32 ou 64 bits)
Méthodes différentes pour passer de la base 10 au cpt2 pour les nombres positifs et négatifs :
- Nombres positifs : pareil que le binaire pour passer de base 10 à 2 (cf page sur la représentation des nombres dans différentes bases
- Nombres négatifs : utilisation du complément à 2
::: tip[Rappel : complément] Le complément à N d’un nombre est le nombre qui permet d’atteindre N. Par exemple : cpt10(3) = 10 - 3 = 7 :::
::: note[Définition plus formelle] Complément à 2 sur k (16, 32, 64) bits mais en réalité on calcule le complément à Complement à 2 en base 10 de N ↪ cpt2(N) = Exemple : cpt2(3) sur 4 bits ↪ cpt2(3) = = 16 - 3 = 13 Donc en base 2 : :::
::: warning[Utilisation du complément à 2] Un nombre négatif est le complément 2 du même nombre positif, donc on utilise le complément à 2 uniquement pour les nombres négatifs Donc si on a -3 en base 10 ↪ on cherche le complément à 2 de 3 cpt2(3) = 1101 donc Alors que :::
::: note[Récapitulatif complément à 2] Représentation utilisée pour les entiers par les ordinateurs bit de signe, S=poids fort (situé à gauche) = MSB
- S=0 : signe positif
- S=1 : signe négatif Nombre de bits fixé (bits restants servent à la valeur de l’entier) :::
Conversion Décimal vers Complément à 2
::: note[Méthode 0 : calcul de ] Calcul de en décimal et conversion en binaire ↪ donne la valeur du nombre négatif en complément à 2 :::
::: tip[Exemple méthode 0]
- Calcul de :
- Conversion en binaire : :::
::: warning[Ne pas confondre format et calcul] Format cpt à 2 : binaire naturel pour les entiers positifs et caclul du complément à 2 pour les négatifs :::
::: note[Méthode 1 (calculatoire)]
- Pour les entiers positifs ↪ binaire naturel (et S=0)
- Pour les entiers négatifs ↪ compléments à 2 (et S=1) Dans les 2 cas : cpt2 = cpt1 + 1 cpt1 = complète à 1 (1 ↪ 0 et 0 ↪ 1) :::
::: tip[Exemple méthode 1] donc (codé sur 1 octect donc 8 bits)
- On part du nombre binaire de 10 : 0000 1011
- Complément à 1 de ce nombre : 1111 0100
- Ajout de 1 : 1111 0101 :::
::: note[Méthode 2 (manuelle)] Bits inchangés de droite à gauche (du LSB ↪ MSB) jusqu’au 1er “1” inclus puis tous les bits suivants sont inversés :::
::: tip[Exemple méthode 2]
- Lecture de droite à gauche de 00001011
- Le LSB dans ce cas est déjà un 1, donc on le conserve et on inverse tous les autres : 11110101 :::
Donc, sur k bits, on peut représenter les entiers de à avec le complément à 2
::: note[Pourquoi ?] Car il y a 1 bit de réservé pour le bit de signe ! (S=0 si positif, 1 sinon) :::
Par exemple sur 3 bits, on va de donc de :
| -4 | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
|---|---|---|---|---|---|---|---|
| 100 | 101 | 110 | 111 | 000 | 001 | 010 | 011 |
::: tip[Différence entre les positifs et négatifs en binaire] Contrairement aux positifs, plus les entiers négatifs sont grands, plus leur correspondance en binaire sera petite en complément à 2 :::
Conversion Complément à 2 vers Décimal
Pour les entiers positifs (S=0) : binaire naturel
::: tip[Exemple pour un nombre positif] à convertir en décimal
- Le bit de signe est égal à 0 donc nombre positif
- On convertit en décimal : :::
Pour les entiers négatifs (S=1) : on reprend le complément à 2
::: tip[Exemple pour un nombre négatif] à convertir en décimal
- Le bit de signe est égal à 1 donc nombre négatif
- On a donc : cpt(N) + 1 = 1100 0111
- On inverse tous les bits : 0011 1000
- On rajoute 1 : 0011 1001
- On convertit en décimal : Ne pas oublier le signe car le nombre est négatif ! :::
::: warning[Attention à respecter le format de cpt2 sur bits] Lors d’une conversion à partir d’un format cpt2, le nombre de bits doit être défini, et il faut absolument respecter le nombre de bits lors de la conversion Le format complément à 2 n’est pas le même selon le nombre de bits utilisés Par exemple : (4 bits, 8 bits, 16 bits) 310 = 0011cpt2 = 0000 0011cpt2 = 0000 0000 0000 0011cpt2 -310 = 1101cpt2 = 1111 1101cpt2 = 1111 1111 1111 1101cpt2 On recopie le bit de signe devant pour respecter le format (donc 0 si positif et 1 si négatif) :::
Evidemment, plus est grand, plus on pourra représenter un nombre d’entiers importants. Donc, il est forcément possible de passer d’une représentation sur bits à une représentation sur bits () mais il n’est pas forcément possible de faire l’inverse.
Opérations sur les entiers en machine avec les Compléments à 2
Nombres de signes opposés
Si les 2 nombres sont de signes opposés ↪ résultat représentable (car on peut représenter de à )
::: tip[Exemple de calcul]
63 - 63 = 63 + (-63) à convertir en complément à 2
 On ne s’occupe pas de la retenue car on représente sur 8 bits donc le résultat est bien 0000 0000
63 - 18
On ne s’occupe pas de la retenue car on représente sur 8 bits donc le résultat est bien 0000 0000
63 - 18
 Le résultat est donc (en ignorant la retenue) : 0010 1101
On ignore la retenue car on effectue en fait le calcul avec le complément à 2 et la retenue ignorée
:::
Le résultat est donc (en ignorant la retenue) : 0010 1101
On ignore la retenue car on effectue en fait le calcul avec le complément à 2 et la retenue ignorée
:::
::: warning[Retenue] La retenue est toujours ignorée, on n’en tient pas compte dans le résultat Elle peut néanmoins être stockée pour effectuer des vérifications si besoin :::
Nombres de même signe
Si les 2 nombres ont le même signe, on risque de dépasser l’intervalle de nombres que l’on peut représenter : on doit donc vérifier le dépassement = overflow
Sur 3 bits par exemple, on ne peut pas représenter 3+3 car le nombre maximal représenté est 3 < 6
::: tip[Exemples de calculs]
Pour chaque calcul, on représente la retenue (carry = C) et le bit de signe S
On se trouve sur 8 bits dans ces exemples donc on peut représenter de -128 à 127
 Résultat : 001010011 donc C = S
On a un résultat de 83 donc le résultat est représentable : pas d’overflow
Résultat : 001010011 donc C = S
On a un résultat de 83 donc le résultat est représentable : pas d’overflow
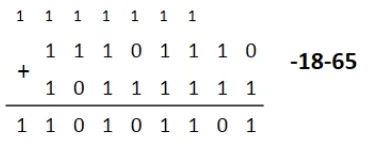 Résultat : 110101101 donc C =S
On a un résultat de -83 donc le résultat est représentable : pas d’overflow
101+65
Résultat : 110101101 donc C =S
On a un résultat de -83 donc le résultat est représentable : pas d’overflow
101+65
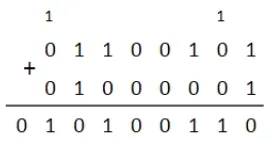 Résultat : 010100110, donc C S
Le résultat est de 166 > 127 donc overflow
-101-65
Résultat : 010100110, donc C S
Le résultat est de 166 > 127 donc overflow
-101-65
 Résultat : 101011010, donc C S
Le résultat est de -166 > -128 donc overflow
:::
Résultat : 101011010, donc C S
Le résultat est de -166 > -128 donc overflow
:::
Il est donc bien nécessaire d’afficher la retenue C pour pouvoir savoir si le résultat est représentable et donc s’il y a dépassement.
Représentation des nombres réels ↪ nombres flottants
Représentation en virgule flottante
Nombre réel = abus de langage sur un ordinateur ↪ plutôt un rationel avec un nombre fini de chiffres
Représentation en virgule fixe (nb de chiffres constants après la virgule) : pose des problèmes avec les petits et grands nombres donc pas utilisable
::: tip[Représentation virgule fixe]
- masse du soleil : 19891 0…0 g (… = 24 zéros)
- masse d’un électron : 0,0…09109 g (…= 25 zéros) Stockage énorme en nombre de bits nécessaires :::
On utilise donc la représentation en virgule flottante
::: note[Réprésentation en virgule flottante]
- basée sur la notation scientifique avec exposant (la virgule flotte)
- nombre représenté de manière compacte Avec les exemples précédents :
- masse du soleil : 1,9891 kg
- masse d’un électron : 9,109 g Ecriture des nombres réels sous forme flottante : avec :
- s ↪ signe (=0 ou 1)
- b ↪ base (en écriture scientifique : base 10)
- e ↪ exposant (ordre de grandeur) qui peut être négatif ou positif
- m ↪ mantisse (chiffres significatifs de ) > 0 :::
::: tip[Application de la représentation] Masse du soleil : 1,9891 kg
- s ↪ 0
- b ↪10
- e ↪ 30
- m ↪ 1,9891 :::
Représentation en norme IEEE1754
Nombres à virgules flottantes en binaire ↪ représentation par le standard IEEE754 pour ecrire le nombre n réel sous la forme :
Le format IEEE754 est une norme définie par :
avec donc :
- s ↪ signe = 0 ou 1
- b ↪base = 2
- e= E-d ↪ exposant 0 (car pas possible de mettre un format si négatif) d est un décalage connu constant
- m=1,M ↪ mantisse
La représentation par le standard IEEE754 s’écrit tel que : SEM(2) avec :
| le signe S (1 bit) | l’exposant E (k bits) | la mantisse M (n-k-1) bits |
|---|---|---|
| 0 ou 1 | e transformé en binaire | chiffres signficatifs |
::: note[Calculer E = exposant]
- E = e+d = exposant biaisé/décale qui est codé sur k bits
- et
- Donc, pour connaître E, on doit connaître d = biais/décalage (dépend du format) = (k est connu = nombre de bits)
- D’où : et (les valeurs de 0 () et de () sont des cas particuliers) :::
::: note[Calculer M = mantisse] Pour un nombre en base 10 tel que : (bit caché qu’on ne représente pas due à la normalisation de la mantisse) On a :::
::: tip[Exemple avec 1ère méthode] Avec k = 3, donc E codé sur 3 bits :
- valeurs de 000 à 111 (de 0 à 7)
- Les valeurs 0 et 7 sont des cas particuliers donc E peut prendre comme valeurs de 1 à 6 (001 à 110 en binaire)
- e (exposant “normal”) va de -2 à 3 (le décalage d est ) Mantisse : sur 3 bits M va de 000 à 111 donc m de 1 à 1,111 Exemple pour convertir dans ce format flottant On divise tout la puissance maximale : , ce qui revient à (ressemble bien à quelque chose de la forme : ) Donc, on a finalement : Donc M = 100 (car on est sur 3 bits) et E = e+d = 2 + 3 = 5 = D’où finalement : 0 101 100 (format IEEE 7 bits) :::
::: tip[Exemple avec 2ème méthode] Méthode moins rigoureuse car on mélange des bases pour représenter le format IEEE754
- 6 en binaire : 110
- On décale la virgule pour avoir un nombre de la forme “1,…” donc : 1,10
- Comme on a décalé de 2 rangs, on multiplie par donc (donc on mélange les bases) On a donc directement :
- M = 10 en décimal donc 100 en binaire
- e = 2 donc comme E = e + d = 2+3 = 5 en décimal donc 101 en binaire Ce qui nous donne 0 101 100 en format IEEE754 :::
::: tip[Exemple avec une troisième méthode] Calcul qui devient vite fastidieux pour de grands nombres
- Trouver la puissance de 2 la plus proche de 6
- Diviser par cette puissance de 2 : donc donc on est déjà sous la forme d’un flottant en puissance de 2
- m en base 10 = 1,5 donc m en binaire = 1,100
- e =2 donc E = 5 en base 10 donc 101 en binaire On retrouve bien le résultat : 0 101 100 en format IEEE754 :::
Format réellement utilisés dans l’ordinateur
Couramment ↪ 32 et 64 bits
| Format | Nb de bits | bits dans S | bits dans E | Décalage d | bits de M |
|---|---|---|---|---|---|
| Simple precision (float) | 32 | 1 | 8 | 127 = | 23 |
| Double precision (double) | 64 | 1 | 11 | 1023 = | 52 |
Avec la double precision : on peut représenter un plus grand nombre de nombre (+ petits et + grands)
Limites de la représentation (32 bits)
 Donc :
Donc :
- Underflow : on ne peut pas représenter des valeurs plus petites que l’ordre de
- Overflow : on ne peut pas représenter des valeurs plus grandes que l’ordre
(On peut utiliser des supercalculateurs pour effectuer les calculs sur des nombres très grands/très petits)
::: tip[Convertir 25,5 en IEEE sur 32 bits] 1ère méthode :
- Décomposition en puissance de 2 : 25,5 = 16 + 8 + 1 + 0,5 =
- Division par :
- Donc e = 4 en décimal donc E = 4 +127 = 131 =
- Pour la mantisse : m = 1,110011 donc M = 10011(0) où (0) représente 18 0 pour arriver à 23 bits au total
- Le nombre est donc : 0 10000011 10011(0) 2ème méthode :
- Passage de 25,5 en binaire : 11001,1
- Sous la forme “1,…” : (décalage de 4 rangs de la virgule)
- Donc e = 4 donc E = 131 =
- M = 10011(0) 3ème méthode :
- Division du nombre décimal par la puissance de 2 la plus proche () donc :
- Ecriture sous le bon format :
- On a bien e=4 donc E = 131
- m=1,59375 en décimal donc on retrouve bien la mantisse en repassant en binaire :::
::: warning[Ne pas oublier le bit caché] m = 1,M, et on ne représente que M en écrivant le nombre sous format IEEE754 Mais la mantisse commence bien par un bit = 1 qui est donc le + significatif mais qui est implicite :::
::: caution[Cas particuliers] Quand E = 0 ou E =
| Cas | Mantisse | Exposant | Signe |
|---|---|---|---|
| Codage du 0 | M = 0…0 | E = 0 | S = 0 ou 1 |
| Codage du | M = 0…0 | E = Emax + 1 (tous les bits à 1) | S = 0 ou 1 (dépend du signe) |
| Codage du NaN2 | M 0…0 | E = Emax + 1 (tous les bits à 1) | S = 0 ou 1 (dépend du signe) |
| ::: |
::: tip[Puissance d’une unité de calcul] Pour calculer la complexité d’un programme : on regarde le nombre d’opérations par seconde sur les flottantes (Floops = Floating poiint Operations Per Second) Les flottants peuvent mener à des erreurs (cf sur python) dans les calculs scientifiques :::
Opérations sur les flottants
- Additions et soustraction ↪ avoir les mêmes exposants (le plus élevé pour conserver l’ordre de grandeur) ↪ peut impliquer une perte de précision
- Multiplication ↪ perte d’information (arrondi au plus près)
::: tip[Affichage des nombres au format IEEE754] On affiche généralement les nombres au format hexadécimal ce qui permet un affichage plus compact (32 bits devient 8 symboles) :::
Additions et soustractions
::: note[Méthode d’addition avec des flottants]
- Convertir les nombres au format IEEE754
- Mettre au même exposant (le plus grand) ↪ passer l’étape si même exposant. Décalage de la mantisse associé à l’exposant le plus petit
- Faire le calcul sur les mantisses sans oublier le bit caché
- Si les nombres de même signe alors addition binaire
- sinon alors cpt2 du négatif
- Remettre sous format flottant en décalant si besoin la valeur de l’exposant :::
Flottants de même signe
::: tip[Exemple d’opération] Calculer 3 + 15
- Convertir les nombres en format IEEE754 sur 32 bits
- 310 = 0 10000000 100(0)2 (avec (0) = 20 zéros) = 4040
- 1510 = 0 10000010 111(0)2 (avec (0) = 20 zéros) = 4170
- Ici l’exposant le plus grand est = 1000 0010
- donc on doit ajouter +2 à pour avoir le même exposant
- Donc décalage à gauche de 2 rangs de la mantisse ↪ (ne pas oublier le bit caché)
- Calcul sur les mantisses = 10,0100000 :

- Remettre sous forme de flottant pour avoir “1,…” : on décale d’un rang vers la droite ce qui ajoute +1 à l’exposant :
- Finalement, on a : 0 10000011 001(0)2 = 4190 000016 avec le signe, l’exposant et la mantisse :::
::: tip[Opérations avec le même signe] Le résultat est le même, seul le signe change. Par exemple, les calculs et auront le même exposant et la même mantisse mais un signe différent (respectivement 0 et 1) :::
Flottants de signes différents
La seule différence est pour l’étape 3 (addition des mantisses), on utilise donc le cpt2 du négatif
::: tip[Exemple d’opération : 3-15]
- mantisse de 3 modifiée :
- mantisse de 15 : Donc on effectue en fait : , d’où la nécessité de calculer le complément à 2 de Donc : , 1 correspond au signe négatif de
- Calcul :
 Le résultat est 10,10…0 qui est toujours négatif (donc S=1)donc à repasser en complément à 2
La mantisse finale est donc : 01,10…0 = m
Le résultat est 10,10…0 qui est toujours négatif (donc S=1)donc à repasser en complément à 2
La mantisse finale est donc : 01,10…0 = m - Dernière étape : remettre sous format flottant
- E =
- M = 10…0
- S =1 Donc 3- = 1 10000010 100 = C140 :::
::: tip[Pour calculer quand signes opposés] Le résultat de et est le même, seuls S change. En général, ou soustrait toujours la mantisse la plus petite donc effectue :::
Les formats dans différents langages
Python 3
- int (pas de format long contrairement au C)
- float
::: tip[Formats dans Python]
- Possible de forcer le typage sous python, avec
a=float(3)(car sinon int) type()permet de connaître le type- Booléens =
boolsous python :::
Utiliser numpy pour le calcul scientifique
En C
Typage obligatoire
- Float/double
- Simple précision
- Double précision
- Signed short int
- Unsigned short int
- Signed long int
- Unsigned long int