Il y a des altérations du message dues au canal de transmission (câble, transmission sans fil…). Par exemple, pour un taux d’erreur de 10 6 10^{6} 1 0 6 10 6 10^{6} 1 0 6
⇒ Altération des données stockées due à la durée de vie du matériel (DVD, disque-dur, mémoire flash)
Le taux d’erreur varie énormément → compris entre 10 − 9 10^{-9} 1 0 − 9 10 − 4 10^{-4} 1 0 − 4
Le principe général de détection et de correction des erreurs est donc :
d’ajouter de la redondance au message à transmettre → différentes manières de le faireet à la réception d’effectuer l’opération inverse → les bits ajoutés sont contrôlés pour éviter les erreurs
Transmettre un numéro de téléphone avec une erreur
Message transmis Message reçu 0654122235 0654122236
Solution → redondance (un chiffre est remplacé par plusieurs lettres) :
⇒ zero six cinquante-quatre douze deux deux trente-cilq (cilq ≈ \approx ≈
Donc : une information concise est difficile à corriger alors que dans une information redondante , on peut détecter et corriger les erreurs
Différents codes
Code détecteur d’erreur → Détecte un certains nombre d’erreurs mais ne les corrige pasCode détecteur et correcteur d’erreur → Détecte et corrige un certain nombre d’erreurs. Taux d’erreur : T = nombre de bits re c ¸ us erron e ˊ s nombre des bits total e ˊ mis T = \frac{\text{nombre de bits reçus erronés}}{\text{nombre des bits total émis}} T = nombre des bits total e ˊ mis nombre de bits re c ¸ us erron e ˊ s
Débits :
Débit binaire (Db) = nombre de bits transmis/s
Débit symbole (Ds) = nombre de symboles transmis/s (en Baud)
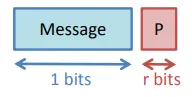
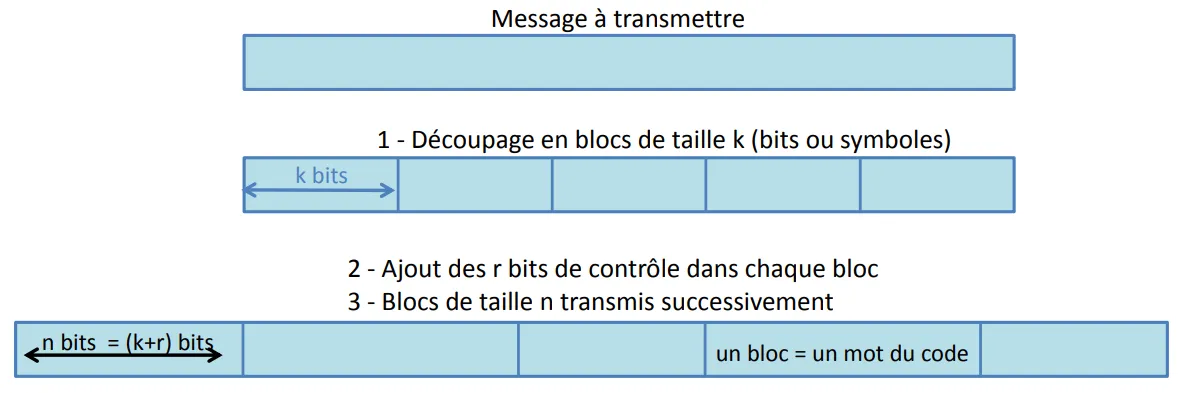
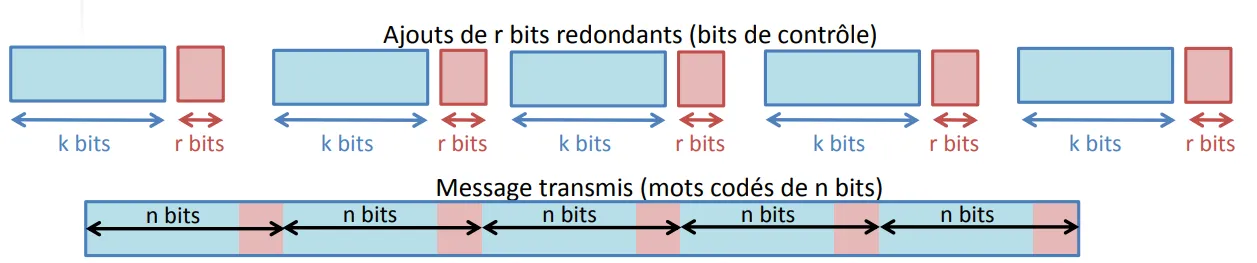
code C(n,k) :
Nombre de bits du message : k bits
Nombre de bits du contrôle : r bits (= redondance)
Nombre de bits transmis : n = k+r bits
Rendement d’un code C(n,k) : R = k N = k k + r < 1 R=\frac{k}{N}=\frac{k}{k+r}<1 R = N k = k + r k < 1
Choix d’un code
Pour une bonne détection/correction d’erreurs → redondance importante donc r grand
Pour un code économique, avec une transmission rapide (débit élevé) → r petit
⇒ Il existe donc un compromis entre l’efficacité de la détection/correction et l’efficacité de la transmission
Dans la pratique des codes correcteurs → codages par blocs
Le mot à coder se trouve au début du mot codé
Il est nécessaire de rajouter r = n − k r = n-k r = n − k
k premiers symboles du mot codé → information
r derniers symboles du mot codé → redondance
Permet un décodage immédiat
Poids de Hamming : p H p_H p H
Distance de Hamming : nombre de positions où les bits sont différents entre 2 mots
Détection et correction d’erreurs avec la distance de Hamming
En connaissant la distance de Hamming minimale d’un code d H m i n d_{Hmin} d H min
Détecter d H m i n d_{Hmin} d H min
Corriger [ d H m i n − 1 2 ] [\frac{d_{Hmin}-1}{2}] [ 2 d H min − 1 ] [ x ] [x] [ x ] x x x
Principe
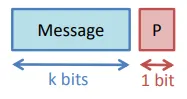
C’est un codage par bit de parité, qui est détecteur d’erreur , très simple et très utilisé
⇒ ajout d’un bit de parité (bit de contrôle) qui correspond au nombre pair de “1”
nombre pair de 1 ⇒ bit de parité = 0
nombre impair de 1 ⇒ bit de parité = 1
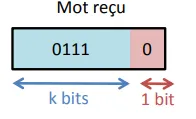
Par exemple, pour le message reçu suivant :
Il y a 1 ou 3 erreurs commises car le nombre de bits est impair
Mais dans cet exemple :
pair
Performances du code de parité
Le code de parité ne détecte qu’un nombre impair d’erreur et la correction est impossible
Longueur des mots d’information : k
Redondance : r=1
Longueur des messages émis : n=k+1
Donc le rendement est tel que R = k k + 1 R=\frac{k}{k+1} R = k + 1 k
Principe du codage par répétition
Codage par répétition du bit à transmettre
Code détecteur et correcteur d’erreur, très simple et très utilisé
Code systématique
Ajout de r bits de contrôles → pour obtenir un nombre de bits impair
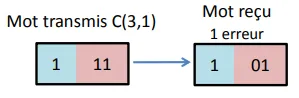
Noté tel que C(n,1) avec n = k+r (et n impair)
Par exemple :
La correction se fait par la distance de Hamming minimale avec les mots possibles (il n’y a que 2 mots possibles), donc le mot décodé est 1.
Dans cet exemple, si il y a 2 ou 3 erreurs ⇒ mauvaise correction
Performances
Détection des erreurs (sauf si tous les bits sont faux ), et correction de r 2 \frac{r}{2} 2 r
Rendement de R = 1 1 + r R=\frac{1}{1+r} R = 1 + r 1 élevé
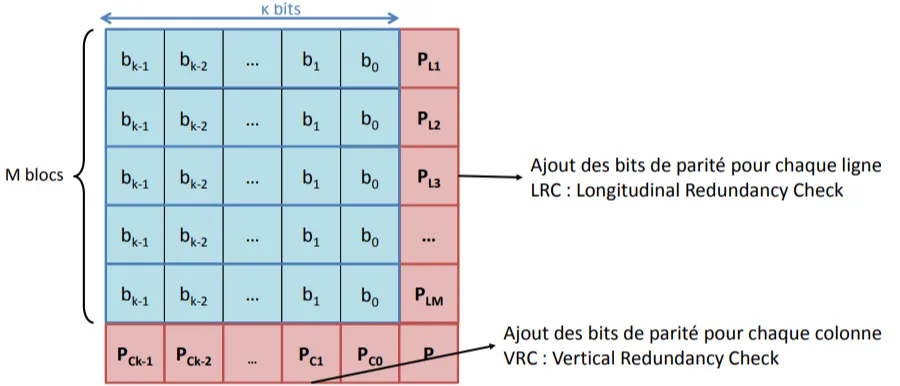
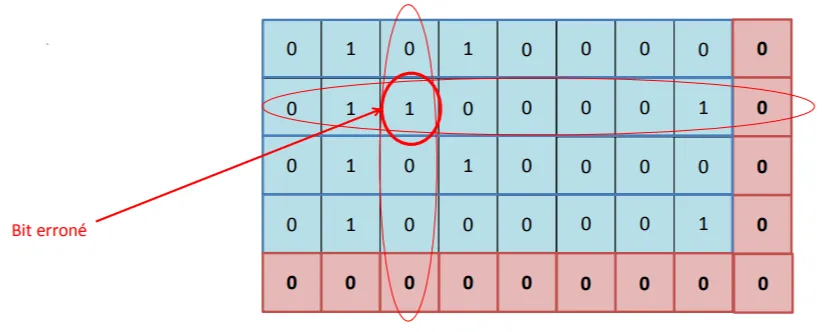
Principe du code double parité
Permet un double contrôle par rapport au codage par rapport au Code de parité , c’est un code détecteur et correcteur d’erreur
Par rapport à la simple parité, on va assembler plusieurs blocs de k bits pour effectuer le double contrôle
Par exemple :
A la réception, on peut donc comparer les bits de parités pour chaque ligne et pour chaque colonne. Le croisement des informations permet de repérer l’erreur :
Performances
Détection de beaucoup d’erreur , mais correction d’une seule erreur
Redondance : 1+k+M (k correspond aux bits de VRC et M aux bits de LRC + le bit au croisement des 2)
Longueur des blocs émis : n = ( M + 1 ) × ( k + 1 ) n= (M+1)\times (k+1) n = ( M + 1 ) × ( k + 1 )
Rendement R = = M k k + M k + M + 1 R=\frac{}{}=\frac{Mk}{k+Mk+M+1} R = = k + M k + M + 1 M k
Donc meilleur rendement que le Code de répétition
Code de Hamming
Le code de Hamming est un codage par bit de parité .
C’est un code correcteur d’erreur grâce à l’utilisation de plusieurs bits de parité. Il permet de détecter la position d’une erreur et est donc auto-correcteur
⇒ pour un mot de k bits → ajout de r bits de contrôle , donc la longueur totale du message est 2 r − 1 2^{r}-1 2 r − 1
On observe que le rendement augmente avec le nombre de bits de contrôle (de 1 3 \frac{1}{3} 3 1 11 15 \frac{11}{15} 15 11
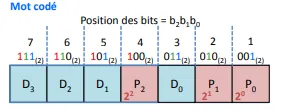
Les bits de contrôle se trouvent sur les positions des puissances de 2 . Par exemple, avec un mot à transmettre tel que :
Le mot codé sera :
Pour décoder, il suffit de re-calculer les bits de parité p 0 ′ p_{0}' p 0 ′ p 1 ′ p_{1}' p 1 ′ p 2 ′ p_{2}' p 2 ′ p 0 p_{0} p 0 p 1 p_{1} p 1 p 2 p_{2} p 2 C 0 C_{0} C 0 C 1 C_{1} C 1 C 2 C_{2} C 2
La lecture de C 2 C 1 C 0 C_{2}C_{1}C_{0} C 2 C 1 C 0 position de l’erreur
C 2 C 1 C 0 C_{2}C_{1}C_{0} C 2 C 1 C 0 Erreur 000 Aucune erreur 001 Position 1 010 Position 2 011 Position 3 100 Position 4 101 Position 5 110 Position 6 111 Position 7
avec les positions telles que :
Remarque sur la position des erreurs
On remarque que la valeur de C 2 C 1 C 0 C_{2}C_{1}C_{0} C 2 C 1 C 0 binaire de la position où se trouve l’erreur
Performances du code de Hamming
Longueur des mots d’information : k k k
Redondance : r r r
Longueur des messages émis : n = 2 r − 1 n=2^{r}-1 n = 2 r − 1
Rendement : R = 2 r − 1 − r 2 r − 1 R = \frac{2^{r}-1-r}{2^{r}-1} R = 2 r − 1 2 r − 1 − r Code qui permet de détecter et de corriger une erreur
Les codes cycliques sont des codes utilisés dans certains cas qui ne corrigent pas les erreurs mais les détectent rapidement et efficacement
Les CRC 1 réseaux informatiques afin de détecter les erreurs groupées
Schéma général du principe du CRC :
Le mot binaire de k bits est représenté par un polynôme de degré k-1
Par exemple :
mot = [ b k − 1 b k − 2 . . . b 0 ] [b_{k-1}b_{k-2}...b_{0}] [ b k − 1 b k − 2 ... b 0 ]
polynôme associé : P ( x ) = b k − 1 × x k − 1 + b k − 2 × x k − 2 . . . b 0 × x 0 P(x)=b_{k-1}\times x^{k-1}+b_{k-2}\times x^{k-2}...b_{0}\times x^{0} P ( x ) = b k − 1 × x k − 1 + b k − 2 × x k − 2 ... b 0 × x 0
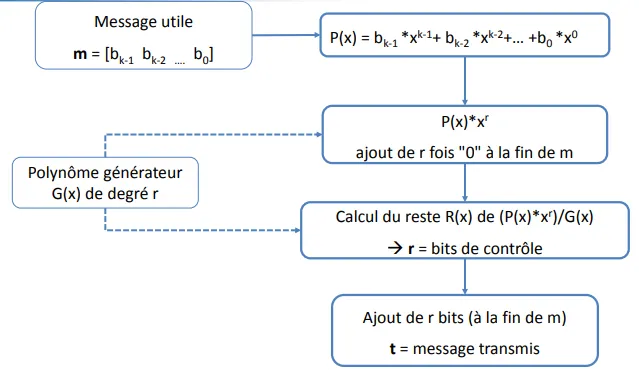
Afin de coder le mot (donc en ajoutant des bits de contrôles), on effectue des opérations sur les polynômes en utilisant un polynôme générateur
Le polynôme générateur G ( x ) G(x) G ( x ) r r r l’émetteur et le récepteur
Calcul de P ( x ) × x r ⇔ P(x)\times x^{r} \Leftrightarrow P ( x ) × x r ⇔ ajouter r r r 0 0 0
Exemple avec k = 5 k=5 k = 5
Le polynôme est de degré k − 1 k-1 k − 1
Soit le mot binaire : [1 0 1 1 1] → P ( x ) = x 4 + x 2 + x + 1 P(x)=x^{4}+x^{2}+x+1 P ( x ) = x 4 + x 2 + x + 1
Soit G ( x ) = x 2 + 1 G(x)=x^{2}+1 G ( x ) = x 2 + 1 r = 2 r=2 r = 2
Donc, P ( x ) × x 2 = x 6 + x 4 + x 3 + x 2 P(x)\times x^{2}=x^{6}+x^{4}+x^{3}+x^{2} P ( x ) × x 2 = x 6 + x 4 + x 3 + x 2 00
Exemple avec k = 5 k=5 k = 5
On calcule donc x 6 + x 4 + x 3 + x 2 x 2 + 1 \frac{x^{6}+x^{4}+x^{3}+x^{2}}{x^{2}+1} x 2 + 1 x 6 + x 4 + x 3 + x 2
Mais sans aucun signe négatif , donc on a :
Le reste de la division de P ( x ) × x r G ( x ) \frac{P(x)\times x^{r}}{G(x)} G ( x ) P ( x ) × x r r r r à la fin du mot à transmettre ce qui correspond au polynôme cyclique T ( x ) T(x) T ( x )
Exemple avec k = 5 k=5 k = 5
D’après l’étape précédente, le reste est x + 1 x+1 x + 1 11 \textcolor{red}{11} 11
Comme le mot initial est 10111 10111 10111 11 \textcolor{red}{11} 11 t = 10111 11 t = 10111\textcolor{red}{11} t = 10111 11
Réception du message t ′ t' t ′ T ( x ) T(x) T ( x )
Opération T ( x ) G ( x ) \frac{T(x)}{G(x)} G ( x ) T ( x ) G ( x ) G(x) G ( x )
Reste de la division :
0 ⇒ pas d’erreur
≠ \neq =
Code détecteur d’erreur Code correcteur d’erreurs (et détecteur) Code de parité Code de répétition Code CRC Code de double parité Code de Hamming
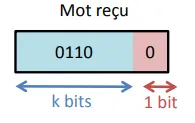Il peut y avoir 0, 2 ou 4 erreurs commises car le nombre de bits est pair
