Objectif de la compression ↪ réduire la longueur d’une séquence numérique (en binaire) sans affecter son contenu informatif (= conservation de l’information)

➡ Transformer l’information délivrée par la source numérique ↪ on doit éliminer les redondances = représentation efficace

Le but est donc :

• de diminuer les tailles de fichiers et l’espace mémoire
• d’augmenter la capacité de transmission (en télécom, afin d’avoir un débit + important)

Il existe 2 types de compression :

1. Compression sans perte ↪ on retrouve l’intégralité des données stockées sous forme comprimée (par exemple : billets pour un concert, déclaration d’impôts, bulletins de votes)
2. Compression avec pertes ↪ un peu de distorsion donc perte d’information mais plus complexe (par exemple : émissions podcasts, musiques au format mp3, photos, vidéos…)

Ici, on ne verra que la compression sans perte.

Codage de caractères

Introduction

Dans les exemples, nous verrons comment compresser du texte, donc il est important de voir comment on peut coder ce texte.

Les ordinateurs utilisent des données binaires, donc chaque caractère de texte va être codé par 1 nombre, donc par une suite de bits.

Il existe différents codages de caractères (évolution avec le temps et différente selon les langues)

codage Baudot (1874) : premier code binaire destiné à être utilisé par une machine

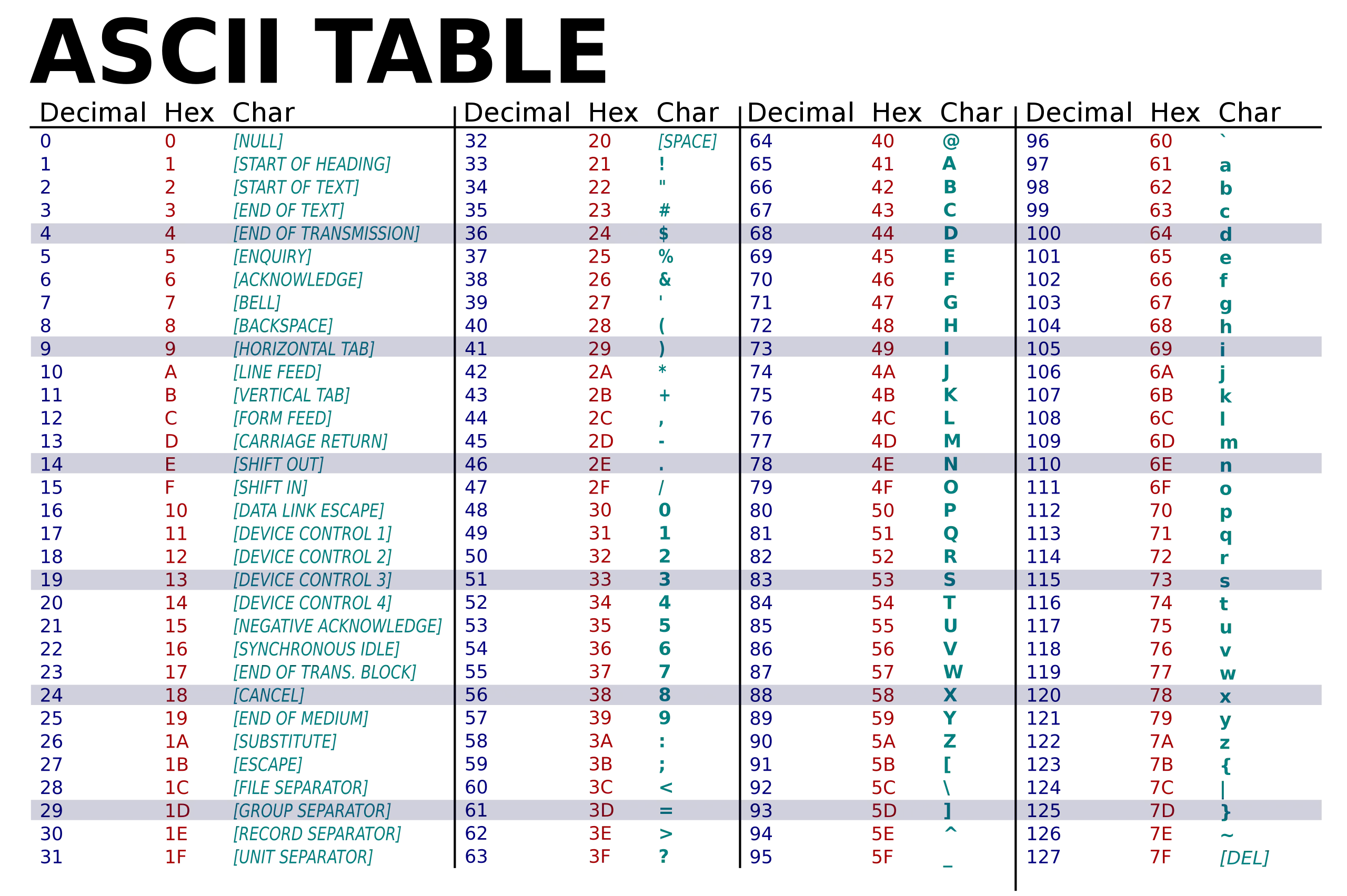
Code ASCII1

Développé dans les années 1960, norme ISO 646 en 1983

Codage qui utilise 7 bits pour représenter un caractère, donc permet de représenter $2^8=128$ caractères différents ce qui représente :

• 26 lettres latines minuscules
• 26 lettres latines majuscules
• 10 chiffres décimaux
• espace
• ponctuation
• parenthèses
• codes de formatage (retour à la ligne, DEL, ESC)

Format : 1 octet par caractère (8ème bits soit à 0, soit un bit de parité pour détecter les erreurs selon les systèmes de transmission : pour l’uniformisation des données)

Donc développement d’autres codages de caractères

Autre codage de caractère (UTF-8)

ISO2 8859

• Versions ASCII étendues : Compatibilités ascendante et descendante (programme de lecture ISO8859 peut lire de l’ASCII et programme ASCII peut lire ISO8859)
• Version la plus utilisée ISO8859-1 souvent dénommée Latin-1 (Europe Occidentale)
• 191 caractères codés sur un octet (au lieu de 128) ;
• Versions ISO8859-2 (Europe de l’est), -3 (Europe du sud), -4 (Europe du nord), -5 (pour le russe), -6 (pour l’arabe)
• Nombreuses versions non compatibles entre elles et insuffisant pour les langues à idéogrammes

Unicode (1987)

• Créer un code universel
• Augmenter le nombre de bits pour coder un caractère ↪ 16 bits (65536 caractères)
• Inconvénients : 2 fois plus gros et non-compatible avec ASCII
• Est devenu une famille de codage
• En 1991, consortium Unicode, la norme Unicode, en plus d’un standard de codage de caractère, un immense rapport sur les langues.
• La version 10.0,(8 518 nouveaux caractères) pour un total de 136 690 caractères est publiée le 20 juin 2017
• Plusieurs encodage existent ↪ le plus connu UTF³ qui est compatible avec ASCII

UTF-8

Codage de longueur variable :

Nombre d’octets	Caractères codés
Sur 1 octet (0x00 à 0x7F)	tous les caractères du ASCII (MSB4 à 0)
Sur 2, 3 ou 4 octets	les autres caractères (MSB à 1)

21 bits sont suffisants pour représenter l’ensemble des caractères définis par l’Unicode

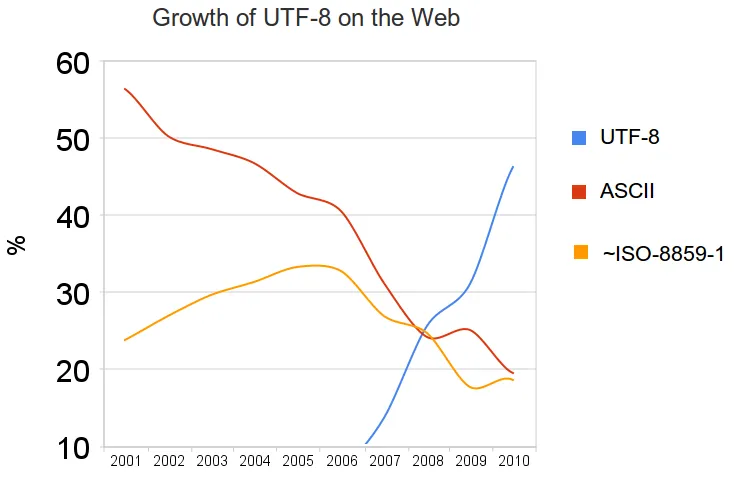
L’UTF-8 domine le web, c’est le codage le plus utilisé actuellement (source)

Compression

Introduction

La distribution des lettres n’est pas équivalente en française (ou dans d’autres langues) :

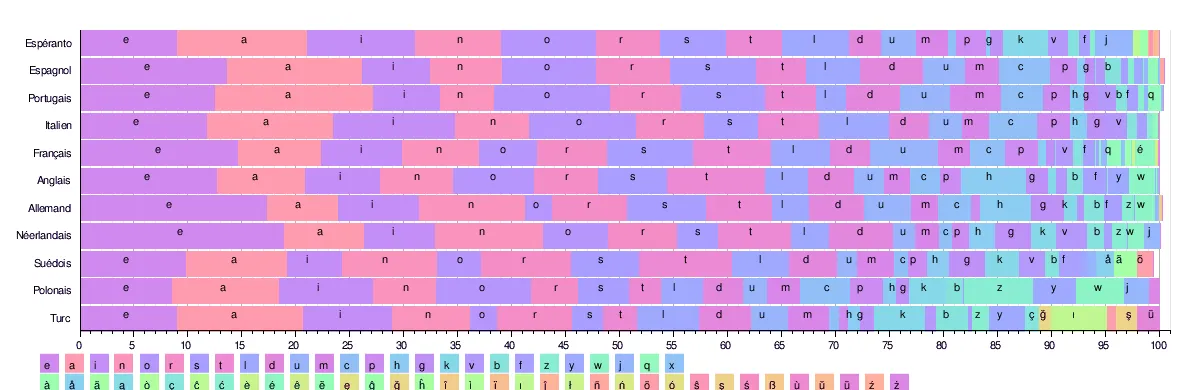Par exemple, la lettre e est utilisée 15 fois plus souvent que la lettre de b.

Premières compressions : Morse, avec les lettres les + utilisés : e, a, t (on voit qu’elles ont un plus court symbole)

Définitions

• La compression transforme l’information délivrée par la source numérique
• Elimine les redondances ↪ pour minimiser la longueur binaire moyenne d’un code $\overline{L}$

Information associée à un symbole

Soit A le symbole dont la probabilité d’occurrence est $p_{A}$. L’information liée à A est :

$$I_{A}=\log_{2}\left( \frac{1}{p_{A}} \right ) = -\log_2p_{A}$$

Donc, si A est peu probable, $I_{A} \rightarrow +\infty$, et si A quasi certain, $I_{A}\rightarrow 0$

Donc, plus $p$ est élevé, plus $I$ sera faible (donc l’information est liée à la rareté d’un symbole)

Entropie H : information moyenne liée au code

L’entropie représente la moyenne pondérée de l’information et est définie par :

$$H = \sum\limits_{k=1}^{Q}p_{k}I_{k}=-\sum\limits_{k=1}^{Q}p_{k}\log_{2}p_{k}$$

L’unité de H est en bits d’information / symbole transmis, ou en Sh (Shannon)

Les valeurs extrêmes de l’entropie sont :

• $H_{min}=0$ pour $p_{k}=1$ (1 seul symbole présent)
• $H_{max}=\log_{2}Q$ pour Q symboles équiprobables, donc $p_{i}=\frac{1}{Q} \forall i$

[!quote] Origines de la notion d’entropie

En physique (Boltzmann⁵, 1872), l’entropie mesure le désordre dans un système.

En théorie de l’information (Shannon ⁶, 1948), l’entropie mesure la “quantité d’information” contenue dans un signal :::

Inégalité de Kraft

L’inégalité de Kraft est un résultat fondamental en théorie des codes, c’est une condition nécessaire et suffisante d’existence d’un code déchiffrable et instantané

Un code instantané doit satisfaire cette inégalité :

$$\sum_{k=1}^{Q}2^{-l_{k}} \leq 1$$

La réciproque est vraie, si une suite de $l_{k}$ vérifient cette relation, alors il existe un code instantané avec cette distribution des longueurs

Autres définitions

Codages de compression statistique

Introduction

Compressions avec algorithmes statistiques

• Pour les données aléatoires ↪ sans corrélations entre elles
• basées sur les fréquences d’apparition des symboles
• attribuer un code binaire d’autant plus court que le symbole apparaît souvent et inversement (appelé VLC⁷) ↪ donc code à longueur variable

Deux algorithmes : de Shannon-Faro et Huffman

Codage de Shannon-Fano

Le codage de Shannon-Fano est un algorithme simple avec des performances élevées. Mais c’est un code sous-optimal (pas optimisé dans le sens statistique) en terme de longueur moyenne des mots code. Donc, pour assurer l’optimalité : code de Huffman

Codage de Huffman

Ce codage a été créé par David A. Huffman, et est par exemple utilisé pour le format .zip

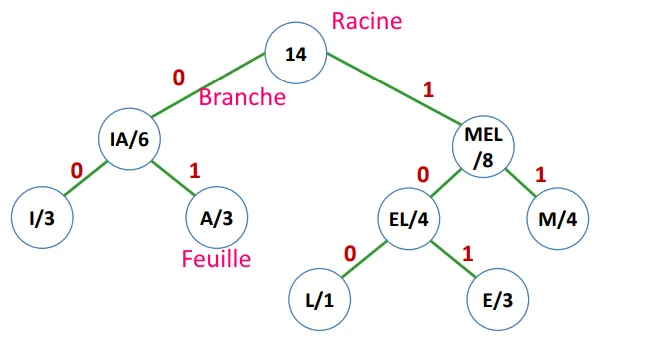
L’idée de ce code est de coder ce qui est fréquent sur peu de place et coder en revanche sur des séquences plus longues ce qui revient rarement. Ce code utilise une création d’un arbre, et l’encodage du texte se fait selon l’arbre.

Illustration d’un arbre du code de Huffman :

Codages par substitution

Précédemment on a vu les compressions avec des algorithmes statistiques.

Les compressions avec des algorithmes dynamiques se font avec :

• des données redondantes : certaines séquences de symboles se répètent plus ou moins régulièrement ↪ leur attribuer un code spécifique bien plus court ⇒ réduire la taille occupée
• RLE et compression par dictionnaire Lempel et Ziv

Codage RLE8

Codage basé sur la redondance

Compression par dictionnaire Lempel et Ziv

Fonctionne sur le même principe que le RLE

Vient de Jacob Ziv and Abraham Lempel (1970) ↪ LZ77, LZ78 et LZW

Conclusion

Plusieurs critères pour qualifier la compression :

• taux de compression
• avec ou sans perte (= destructive ou non)
• temps de compression

Tout algo de compression possède un algo de décompression correspondant

Compression de données sans perte

• réduit la taille des données en supprimant les redondances
• processus réversible, valable pour tout type de données, gain théoriquement assez faible
• compress d’UNIX et format GIF⁹ ↪ Algo LZW (plus efficace que l’algo RLE pour BMP)
• PNG et gziputilisent l’algo Deflate = combinaison des algo LZ77 et Huffman

Compression avec perte

• Compression dégradante, suppression des informations “peu significatives, inutiles”
• Compression non réversible, gain de compression très grand

Format JPEG[^10] : formules mathématiques complexes ↪ enlever les détails non visibles à l’oeil (même principe pour les mp3) [^10] : Joint Photographic Expert Group

Format MPEG[^11] : compression de la vidéo ↪ détecter des corrélations dans les données (informations redondantes)

• corrélations spatiales : des formes qui se répètent, des motifs
• corrélations temporelles ↪ éléments semblables d’une image à l’autre (détection de mouvement) [^11] : Moving Photographic Expert Group

Footnotes

1. American Standard Code for Information Interchange ↩

2. International Organization for Standardization ↩

3. Universal Transformation Format ↩

4. bit de poids fort : non utilisé en ASCII ↩

5. ardent défenseur de l’existence des atomes père de la physique statistique ↩

6. mathématicien, ingénieur électricien, cryptologue père de la théorie de l’information ↩

7. Variable Length Code ↩

8. Run Length Encoding ↩

9. Graphic Interchange Format ↩