Table of Contents
Variables et fonctions logiques
On parle de circuits numériques / logiques (en opposition avec les circuits analogiques qui sont convertis en grandeurs numériques) ⇒ 2 états possibles, par exemple :
- contact ouvert ou fermé
- transistor bloqué ou saturé
Donc il y a un certain nombre de valeurs possibles ( des circuits analogiques).
Ces circuits sont facilités par l’utilisation de l’algèbre de Boole ⇒ manipule des variables qui ne peuvent prendre que 2 états : 0 ou 1
Donc, pour variables binaires indépendantes , une fonction logique est une fonction qui, pour chaque combinaison des variables binaires, prend un état 0 ou 1.
Portes OU, ET, NON
L’algèbre booléenne est plus facile à manimuler que l’algèbre ordinaire parce qu’il n’y a que 2 valeurs possibles ⇒ pas de fraction, de partie décimale, de nombre négatif, de racine carrée…
Fonction logique OU
Opération qui a au moins 2 entrées et sa sortie est 1 si au moins une des entrées est 1, avec une table de vérité :
| A | B | A+B |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
Deux symboles possibles pour OU :
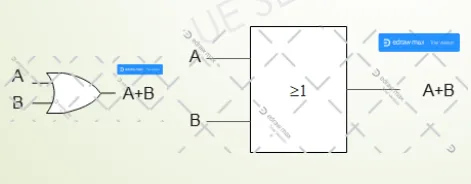
Exemple d’utilisation du OU
Dans certains systèmes de régulation industriels, on veut que la fonction de sortie se mette en marche quand une des valeurs entrées dépasse un seuil. Par exemple, dans un procédé chimique, l’alarme doit se déclencher quand la température dépasse une valeur maximale OU quand la pression dépasse une certaine limite.
On aura alors le montage suivant :
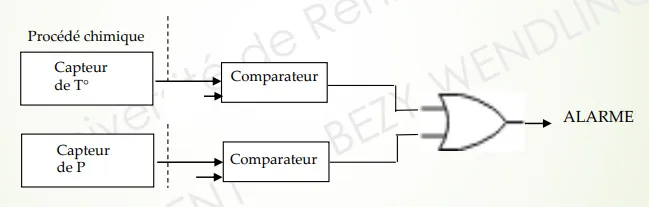
Dans ce système, la sortie des comparateurs passe à un niveau logique 1 quand la température atteint la température maximale (idem pour la pression P).
Composants : les constructeurs de circuits intégrés proposent les boîtiers suivants :
- 4 portes OU à 2 entrées : CI 7432
- 6 portes OU à 2 entrées : CI 74832
Fonction logique ET
Opération avec au moins 2 entrées, la sortie est dans l’état 1 si et seulement si toutes les entrées sont à 1 (donc même règles que la multiplication classique)
Table de vérité :
| A | B | A‧B |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
2 symboles possibles :

Exemple d’utilisation du ET
Déterminer la sortie de la porte ET suivante pour les formes d’ondes des entrées :
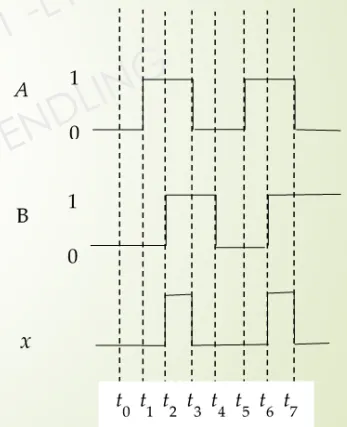
Donc égal à 1 seulement quand A et B sont égaux à 1 en même temps : intervalles et
Fonction logique NON
Opération avec une seule entrée et une seule sortie. Le NON prend l’état 1 si et seulement si son entrée est à 0.
Table de vérité
| 0 | 1 |
| 1 | 0 |
Symboles possibles :
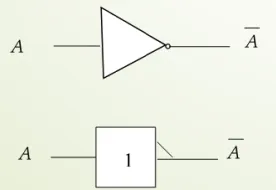
Théorèmes de De Morgan
Deux théorèmes importants :
Ces théorèmes permettent de simplifier des expressions :
-
une fonction
ETpeut être fabriquée à partir deOUetNON -
une fonction
OUpeut être fabriquée à partir deETetNON -
On peut écrire avec la première forme :
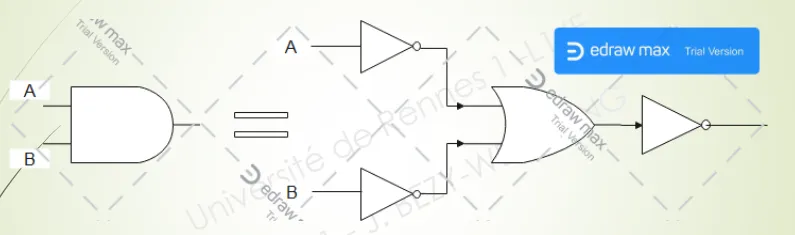
- On peut écrire avec la première forme :
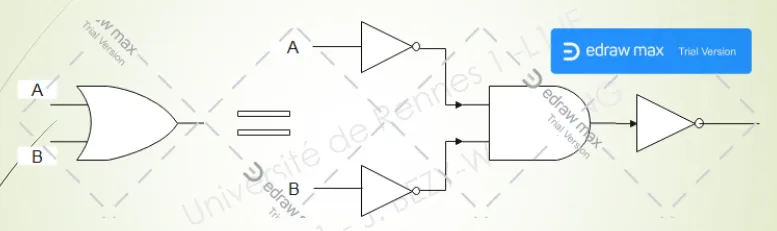
Démonstration de
En appliquant le théorème : Et :
Fonctions logiques NON ET, NON OU, OU EXCLUSIF
Fonction logique NON ET (NAND)
Porte constituée par un inverseur à la sortie d’une porte ET. Portes très utilisés dans la réalisation des circuits logiques. Toute expression logique est réalisable en n’utilisant que des portes NAND
La table de vérité est l’inverse de la table de vérité du ET
| A | B | |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
2 symboles possibles :
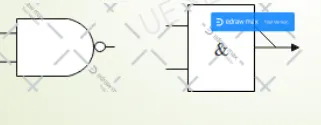
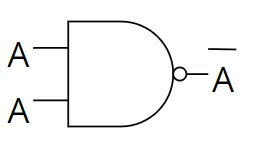
Réalisation du NON avec des NAND
, on veut montrer qu’on peut arriver à avec des NAND
On peut réécrire donc :
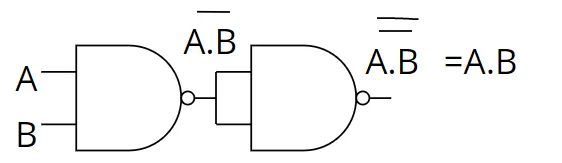
Réalisation du ET avec des NAND
ce qui correspond à la négation de NAND, donc :
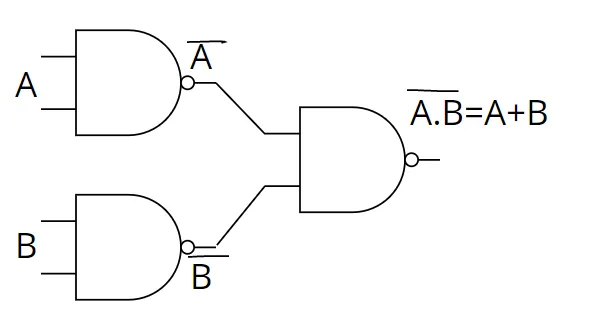
Réalisation du OU avec des NAND
, donc on voit apparaître une fonction NAND avec et
Exemple d’utilisation des portes NAND pour réaliser un circuit quelconque
Doit réaliser un circuit dont l’expression est Contraintes : il doit utiliser le moins de circuits intégrés (CI) possible
Hypothèses : CI disponibles suivants :
- 1 boîtier 7400 (4portes
NAND2 entrées) - 1 boîtier 7408 (4portes
ET2 entrées) - 1 boîtier 7432 (4portes
OU2 entrées)
Solution 1 : directe avec les portes ET, OU
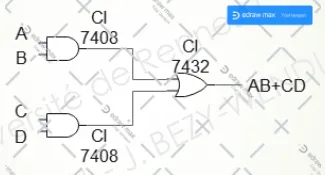
Solution 2 : avec des portes NAND uniquement
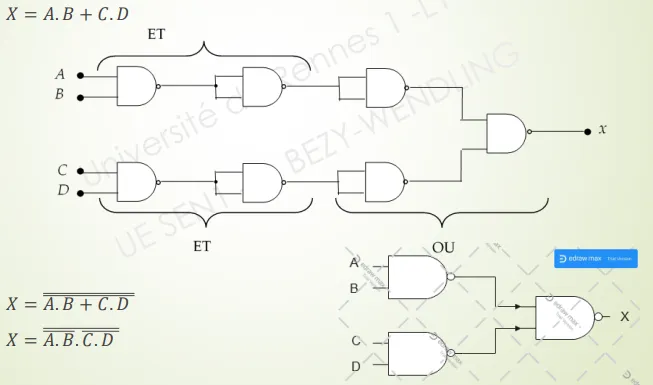
Fonction logique NON OU (NOR)
Une porte NOR a un fonctionnement analogue à une porte OU suivie d’un inverseur : expression de sortie
Table de vérité inverse du OU :
| A | B | |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 0 |
Symboles :
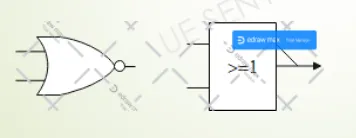
Réalisation du NON avec des NOR
On a donc on peut utiliser 1 seul NOR

Réalisation du OU avec des NOR
donc on a besoin d’inverser avec 1 NOR, puis de ré-inverser avec un autre NOR$

Réalisation du ET avec des NOR
donc on inverse et en utilisant 1 NOR pour chacun et on les additionne avec 1 NOR

Exercice d’application de la fonction NOR
Forme d’onde de sortie de la porte NOR par rapport à celles de ses 3 entrées en fonction du temps :
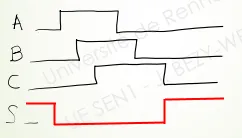
Fonction logique OU EXCLUSIF (XOR)
Fonction logique égale à 1 si on a un nombre impair de 1 à l’entrée La sortie d’une fonction OU EXCLUSIF (XOR) à deux entrées est dans l’état 1 si une entrée et seulement une est dans l’état 1 ↔ niveau haut en sortie quand les signaux sur les deux entrées sont opposés
Table de vérité :
| A | B | |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
[!important] Egalité du
XOR
2 symboles différents :
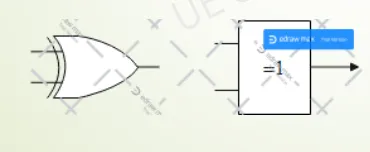
La fonction XOR existe en circuit intégré (7486)
Fonction NON OU EXCLUSIF
Cette fonction s’appelle aussi fonction coïncidence, elle existe comme circuit intégré (CI 74LS266)
Elle peut s’écrire :
Sa table de vérité est l’inverse du XOR
Ses symboles sont :
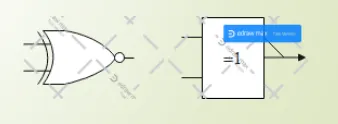
Exercices d’applications
Exercice 1
Complétez les théorèmes de Boole suivants. X représente une variable binaire prenant soit la valeur 0, soit la valeur 1
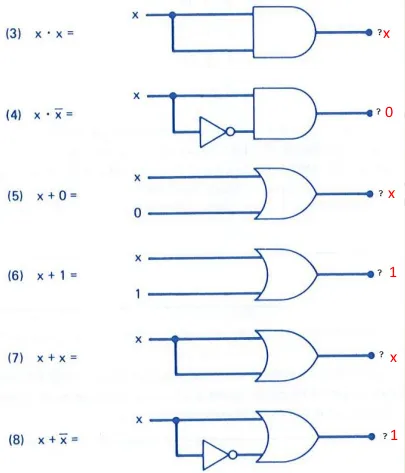
Exercice 2
a) En utilisant les propriétés vues pendant le cours, donner une autre expression de z, qui sera plus simple : b) Même question pour x :
a) donc
b) , et d’après les Théorèmes de De Morgan, donc
Exercice 3
Démontrez les théorèmes de De Morgan, en utilisant tous les cas possibles.
| A | B | ||||
|---|---|---|---|---|---|
| 0 | 0 | 1 | 1 | 1 | 1 |
| 0 | 1 | 1 | 0 | 1 | 1 |
| 1 | 0 | 0 | 1 | 1 | 1 |
| 1 | 1 | 0 | 0 | 0 | 0 |
Exercice 4
Tracer le schéma logique correspondant aux expressions suivantes, en utilisant les portes logiques OU, ET et NON :